Infinite Cache, Finite Request Stream

  In this section we investigate the cache hit-ratio as a function of the number of requests and show that the observed property that the function is logarithmic is derivable from the Zipf model.

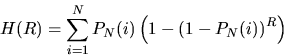
We consider the case where the cache has unlimited storage, so all previously requested pages remain in the cache. In this case, we consider a finite request stream of R requests, and wish to determine the probability that the next request, the R+1'th request, is a request for a page that already resides in the cache. The hit-ratio H(R) can be calculated as follows. If the R+1'th request is for page i then the probability that this page is in the cache is given by (1 - ( 1 - P_N(i))^R). Thus, we have:

$$H(R)=\sum_{i=1}^N P_N(i) \left( 1 - \left( 1 - P_N(i) \right)^R \right)$$

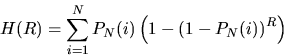
The asymptotic behavior of the hit-ratio is $H(R) \approx \Omega \ln R$. This behavior can be seen more directly by approximating the sum for H(R) by assuming the function $f(i)=(1 - ( 1 - \frac{\Omega}{i})^R)$ is given, for $1 \ll R \ll N$, by:

$$f(i) = \left\{ \begin{array} {ll} 1, & \mbox{if $i \leq R\Omega$} \\ 0, & \mbox{otherwise} \end{array} \right.$$

Then we have

$$H(R)=\sum_{i=1}^N \frac{\Omega}{i} f(i) \approx \sum_{i=1}^{R\Omega} \frac{\Omega}{i} \approx \Omega \ln (R\Omega)$$

We found that the approximation $\Omega \ln (R\Omega)$ underestimates H(R) and that the approximation $\tilde{H}(R) = \Omega \ln R$ is more accurate. Note that when $R \approx N$ this approximation is no longer valid because H(R) approaches unity while $\tilde{H}(R)$ is unbounded. This result that the hit-ratio is logarithmic is consistent with previously observed behavior [GB97,CI97,DMF97].

  

Figure 1: Hit-ratio as a function of the number of requests.

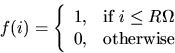
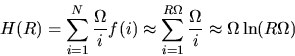
Figure 1 shows the hit-ratio H(R), the approximate hit-ratio $\tilde{H}(R)$ and the hit-ratio for a cache trace as a function of $\ln R$.The cache trace data was collected by Pei et al. using a cache simulator and a Web cache trace file [CI97]. Figure 4 of [CI97] actually plots the hit-ratio as a function of group size, but in the simulation the number of page requests is proportional to the group size.