Finite Cache, Infinite Request Stream

  In this section we investigate the cache hit-ratio as a function of the size of the cache and show that the observed property that this function is logarithmic is also derivable from the Zipf model.

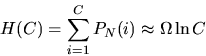
We consider a finite cache with a capacity of C Web pages subject to an infinitely long request stream. We assume that the cache can hold C Web pages regardless of the size of each Web page. Furthermore, we assume that the cache holds the C most popular pages as indicated by the ordering i. The ordering can be determined by measuring the request frequency of each page, which is equivalent to assuming that the cache has a Perfect-LFU page removal policy (see section 7 for a discussion of Perfect-LFU).

We are interested in the asymptotic hit-ratio H(C), which can be calculated to be:

$$H(C) = \sum_{i=1}^C P_N(i) \approx \Omega \ln C$$

This result is consistent with previously observed behavior that the hit-ratio increases logarithmically as a function of cache size [ABCdO96,Gla94,CI97,WAS+96,GB97,RV98,CBC95,DMF97]. For example, Glassman showed this result by using a cache simulator and modelling the requests by a Zipf distribution [Gla94]. Rizzo et al. also published results of hit-ratio as a function of cache size [RV98]. Although they do not compare their graphs to logarithmic functions, we replotted their graphs against a logarithmic scale and found that the graphs were indeed logarithmic.

  

Figure 2: Hit-ratio as a function of cache size.

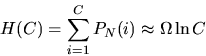
We also provide empirical results for the hit-ratio observed in several trace files. Figure 2 shows the hit-ratios for Web caches using the LRU replacement algorithm for the client traces gathered at Boston University, traces gathered at Virgnia Tech, and two groups of traces, DEC-U1 and DEC-U2, that are gathered at Digital Equipment Corporation. (For details of the traces see [CI97].) The figure shows that the hit ratio clearly grows proportionally with

$$\ln C$$

.

However, the curves do not exactly start from the origin. In other words, if we compare these curves to straight lines running through the coordinate (1,0), it would appear that the model is not particularly accurate. There are a number of reasons for this discrepancy. First, the model does not take into account document modifications at all, while the simulations that generate these hit ratios always treat modified documents as cache misses. It is known that document modifications tend to reduce Web cache hit ratio significantly [KLM97]. Thus, the model will predict a cache hit ratio that is much higher than in practice. We are working on incorporating document changes in the model. Second, the ``cache size'' C in the above figure is not accurate. The simulations were run assuming a cache that has a fixed capacity in terms of bytes, while the Web pages have different sizes. Thus, C in the figure is simply an estimate of the average number of documents in cache. We are planning to run more simulations assuming caches that hold a fixed number of documents to further verify the model.

Lastly, note that the slope of the curves are not necessarily identical because the slope of the approximation for H(C) is dependent on N. The traces were taken during different time periods (Nov. 1994 for Boston University traces, Feb. 1995 for Virginia Tech traces, and Aug. 1996 for DEC traces), and N probably increases with time.