Page Request Interarrival Times

  We now investigate the distribution of times between requests for a given page and show that the probability that a page will referenced k requests after it was last referenced is proportional to 1/k.

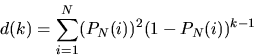
Let us consider an infinite arrival stream and consider a request for a given page i. The quantity of interest is the probability distribution d(k) that the next request for that page is k requests later (i.e. , that the request for page i is followed by k-1 requests for pages other than page i, followed by another request for page i). Assuming that page requests are independent, we find that

$$d(k)=\sum_{i=1}^N (P_N(i))^2 (1-P_N(i))^{k-1}$$

Inserting the Zipf law gives us:

$$d(k)=\sum_{i=1}^N \left(\frac{\Omega}{i}\right)^2 \left(1-\frac{\Omega}{i}\right)^{k-1}$$

Noting that $\Omega \approx \frac{1}{\ln N}$ we have:

$$d(k) \approx \frac{1}{k \ln N} \left( \left(1-\frac{1}{N \ln N}\right)^k - \left(1-\frac{1}{\ln N}\right)^k \right)$$

Note that for $N \ln N \gg k \gg \ln N$, $d(k) \approx 1/(k \ln N)$.

  

Figure 3: Probability distribution for page request interarrival times.

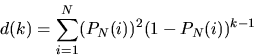
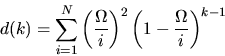
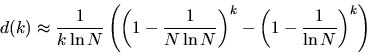
Figure 3 shows a plot of the probability distribution for page request interarrival times d(k) produced by our model and the distribution for a cache trace of actual requests for web pages. The cache trace was extracted from the trace file for a DEC Web server that serviced roughly 1700 workstation over a period of 25 days [DEC96]. Once again the model predicted by Zipf's law is consistent with data observed at operational web servers [RV98,CI97], that is, the probability that a document will be referenced k requests after it was last referenced is proportional to 1/k. Note that our model predicts higher values for d(k) when k < 10² but is quite accurate when k > 10².