Approximating data with polynomials using Matlab

Approximating data points involves selecting a function 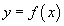such that 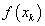comes close to 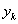Common functions to use are polynomials.

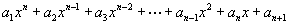
If there are n+1 data points then this nth-degree polynomial will interpolate the data that is the function will pass through each point. For approximation more commonly the polynomial will be of low degree, such as a linear function, and there are many data points. In this case the approximating polynomial is meant to come close to the data, which might be statistically scattered around a linear trend.

Matlab conveniently computes the coefficients of a polynomial that comes close to a set of data points in the least squares sense. If x and y are vectors of n+1 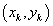data values entered into Matlab, then the function polyfit

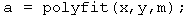
returns the coefficients of a polynomial of degree m that approximates the n+1 data points in vectors x and y. The variable a is a vector of length m+1 that holds the coefficients

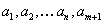
With these coefficients a linear polynomial for instance could be written in Matlab as

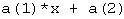
However, Matlab has a more convenient way to evaluate a polynomial with coefficients computed by polyfit. This is with a companion function called polyval.

If x_values is a vector of x values, then the polyval function uses the coefficients in the a vector to compute the value of the polynomial at each of the x values and returns these results to the vector y_values.