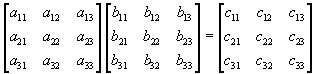Matrix and vector notation

The mathematical subject of linear algebra uses a shorthand notation called matrix and vector notation. Using matrices and vectors, linear systems of equations can be conveniently represented and the operations required to solve the equations can be easily applied to this shorthand notation. The linear system of equations given by

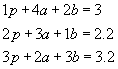
is represented in matrix and vector notation as

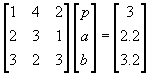
The first set of brackets is a3x3 matrix. The second set of brackets is a 3x1 matrix or is called a column vector. The third set of brackets is also a column vector. Matrix dimensions are quoted as rows x columns.

On the left side of the equation the product of the matrix and vector is accomplished by processing across the first row of the matrix and down the first (and only) column of the vector, multiplying each coefficient with a corresponding variable and summing the three resultant products. This is set equal to the element of the vector on the right side of the equation (circled). Thus you can see that this notation and its process for multiplying matrices and vectors allow us to represent the first equation in the linear system.

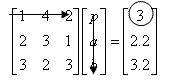
We can then perform the same process on the second row of the matrix. Multiply the second row of coefficients with the first column of variables and sum the three products and set these equal to the second term on the right hand side (circled).

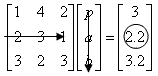
We then perform the same process on the third row of the matrix.

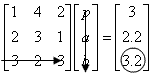
Thus the linear system of equations is represented by this combination of a 3x3 matrix and two 3x1 matrices or column vectors.

In general, matrix multiplication is accomplished by the following algorithm. First you can only multiply a MxN matrix with a NxQ matrix to form a MxQ resulting matrix. That is, the number of columns in the first matrix must equal the number of rows in the second matrix. Usually we are multiplying so-called square matrices where there are equal numbers of rows and columns, so this is not a issue. Or we are multiplying a square matrix by a column vector with the right number of rows.

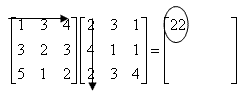
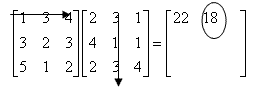
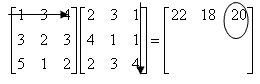
The complete matrix multiplication is

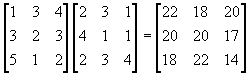
Each element of a matrix is denoted by a double subscript that specifies its row and column position.

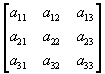
The matrix multiply operation can then be represented mathematically as