Examples:

1. Find the unique values of variables a, b, and c.

   1a+2b+3c=18.1
2a-2b+4c=14.2
3a+5b-2c=6.9


   Equation two minus two times equation one yields 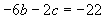While equation three minus 3 times equation one becomes 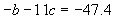Next, we use these two new equations to solve for the variable c by eliminating b as shown below. 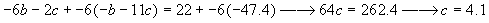Plugging this value into either of the equations with variable a removed yields b=2.3. Plugging found values for c and b into any of the original 3 equations will cause an outcome of a=1.2.

2. Find the unique values of variables a, b, and c.

   3a+2b+3c=11.5
2a-2b-c=1.6
4a-2b-c=11


   Equation one plus equation two becomes
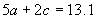
   Equation one plus equation three becomes

   Comment: Notice variable elimination order is not important.

   Using these two calculated equations one can solve for a by subtracting four times the first calculated equation from the second calculated equation. 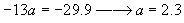Plugging the a value into either of the calculated equations gives . Finally plugging in numerical values of a and c into any of the original equations gives the result b=1.1.