Exercises

Write pseudocode or MATLAB to answer each question.

1. 

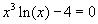
   Here are the steps to complete this exercise:
Plot the function to find starting point
Obtain the successive approximation formula
Choose and apply the formula

2. Write some pseudocode to compute the next approximation of a root of an expression or function based on Newton's Method.

   To get you started, determine what terms and values you need, assign those values and compute the next approximation.

   In the case of Newton's Method, you need an initial guess, the value of the expression at that guess and the value of the derivative at that guess.

   One person's pseudocode may look like this:

   1. Assign an initial guess value to a variable named curr_x.
   2. Assign the value of the expression at curr_x to a variable named f_at_x.
   3. Assign the value of the derivative of the expression at x to a variable named fprime_at_x.
   4. Compute the value of the next approximation using Newton's method and assign this to next_x.

   Notice how wordy the above pseudocode is. Most programmers do not require this much detail in their pseudocode and would instead write something shorter like:

   1. Initialize x (initial guess).
   2. Compute fx at x.
   3. Compute fprimex at x.
   4. Compute the next approximation using Newton's Method.

3. Modify the above pseudocode so that it continues approximating the root until two successive root approximations are within one-one thousandth of each other.

   1. Initialize error_threshold to 1/1000
   2. Initialize current_guess as initial guess.
   3. Initialize second_to_last_guess as current_guess + 2*error_threshold.
   4. while difference between current_guess and second_to_last_guess is greater than error_threshold:
      1. Compute fx at current_guess.
      2. Compute fprimex at current_guess.
      3. Compute next_approximation using Newton's Method.
      4. Assign current_guess to second_to_last_guess.
      5. Assign next_approximation to current_guess.
   5. Display next_approximation as this is the last approximation completed.
   6. Test your last root approximation value by computing the value of the function at that value and comparing this result to zero.

   Adding a "while" loop is a good way to allow this approximation code to continue to execute while our last two approximations are "too far" apart. Caution: it is critial that you initialize the condition variables correctly before the loop, test them correctly at the start of the loop, and update them correctly within the loop to avoid infinite loops.

   If the result of the final test value is not sufficiently close to zero, than one of several things may have occurred:

   • You didn't implement the conditional expression for the while loop correctly.
   • Newton's Method was not correctly implemented
   • Your error_threshold was too large.
   • The function is not continuous or does not cross the x-axis
   • Your initial guess is poor. It must be on a part of the curve that does cross the x-axis without changing direction.