Examples:

1. Estimate the integral of the function 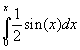using Simpson’s Method with N=4 and thus h= /4. This integral is of course equal to 1.

   f(0)	0
   f( /4)	0.3535533
   f( /2)	0.5
   f(3 /4)	0.3535533
   f( )	0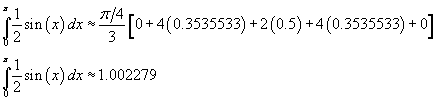

   

   Thus the error is

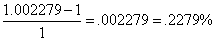
2. Use the same intergral but now use N=8 subintervals and h= /8.

   f(0)	0
   f( /8)	0.1913417
   f( /4)	0.3535533
   f(3 /8)	0.4619397
   f( /2)	0.5
   f(5 /8)	0.46193975
   f(3 /4)	0.3535533
   f(7 /8)	0.19134174
   f( )	0

   

3. We expect that when we increase the number of intervals by a factor of 2 (8/4=2), that our error will be reduced by a factor of 2⁴=16. That means that our answer will be 16 times more accurate, or our error will be 1/16 of the error in the first approximation.

   Let's see if that's the case for this example.

   Recall, that the error when N=4 was

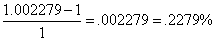
   We can now compute the error when N=8. It is ~0.01%

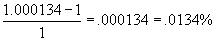
   which is approximately 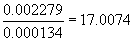times better than the approximation with N=4.

   This result is comparable to the 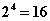improvement we would expect when we increase the number of intervals from 4 to 8.