Examples
Revise Newton's Method from the previous unit to make it work for any function. Instead of putting the code to compute the function and its derivative in the
Newtonfunction definition, use thefcnchkfunction to create function handles that can then be used to compute the desired values. Or, you can write new functions and pass the name of those functions to yourNewtonfunction.function x_next = Newton( x_current, f_x , dx_x ) f = fcnchk( f_x ); dx = fcnchk( dx_x ); x_next = x_current - f(x_current) ./ dx(x_current);
Use your new form of Newton's method to approximate the root of
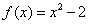
This code fragment uses our revised
Newtonfunction to display the first seven approximations:disp(' Guess #0 = 1'); x = 1; for n = 1:7 x = Newton( x, 'x^2-2', '2*x' ); disp([ 'Approximation #' num2str(n) ' = ' num2str(x,25) ]); endHere's a transcript of the results of executing the above code fragment.
Guess #0 = 1 Approximation #1 = 1.5 Approximation #2 = 1.4166666666666667 Approximation #3 = 1.4142156862745099 Approximation #4 = 1.4142135623746899 Approximation #5 = 1.4142135623730951 Approximation #6 = 1.4142135623730949 Approximation #7 = 1.4142135623730951

