Examples

1. Find the roots of the function

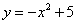
   First, plot the function. The range -3 to 3 will show the roots we are interested in.

   

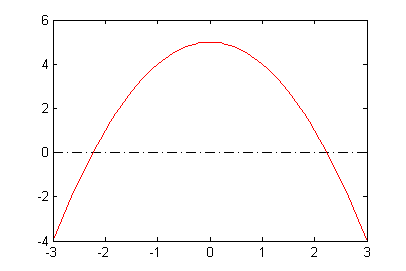
   Place this code in a new m-file and run to see the plot shown here.

   % Find and plot the roots of y=-x^2+5 from -3 to 3
   xx = -3:0.1:3;
   yy = -xx.^2 + 5;  % element-wise for vector use
   plot([-3 3],[0 0],'-.k', xx,yy,'r-'); 
   

2. Use fzero to find the roots of the function in Example 1. Place this code in the same m-file as you created for Example 1:

   % Find the roots of the function y=-x^2+5 and save them in vectors x and y
   x0 = [-2 2];    % initial guesses for the roots
   
   for n = 1:length(x0)
       x(n) = fzero('-x^2+5',x0(n));  % find the root and save it in x
       y(n) = -x(n)^2 + 5;            % evaluate at that root
   end
   
   % Plot the function and the roots
   hold on
   plot( [-3 3],[0 0],'-.k', xx,yy,'r-' ); % plot y=0 and the curve
   
   % Display each root and a label for it on the plot
   for n = 1:length(x)
       plot( x(n), y(n), 'bo' );
       text( x(n)-0.5 , y(n)+0.5 , ...
           ['(' num2str(x(n),3) ',' num2str(y(n),1) ')' ] ); 
   end
   hold off
   

   Here is the figure that is produced, showing the curve and its roots.

   

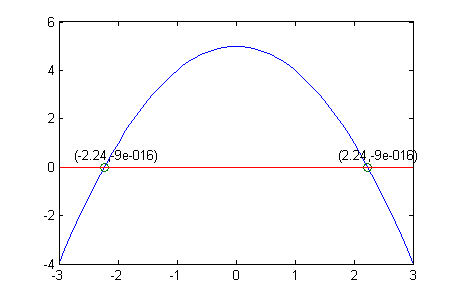
3. Find the roots of the function 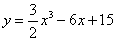A plot of the function is shown for your convenience.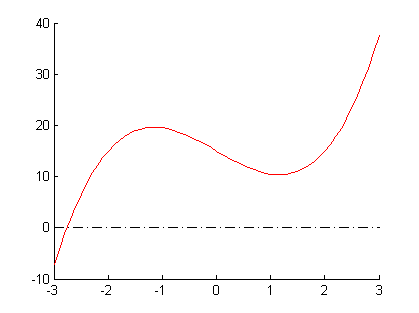

   

   This command will find the root near -3

       >> fzero( '3/2*x.^3-6*x+15', -3 );