Examples
Considering the parachutist jumping from an airplane problem. The first ODE we consider is for the velocity of the parachutist. The forces on the parachutist are the pull of gravity and the drag from the air. To a good approximation, the drag is proportional to the velocity. From Newton's law that the mass times acceleration is equal to the force, we have
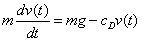 where m is the mass of the parachutist, g is the acceleration due to gravity,
cD is the drag coefficient, and v(t) is the velocity.
For this case, the velocity is positive even though the person is going down.
For this problem we will use metric units: the parachutist weighs 70 kilograms,
the drag coefficient is 10 kg/sec, and the gravitational acceleration is 9.8 m/sec2.
At time 0, the velocity is 0 m/sec.
where m is the mass of the parachutist, g is the acceleration due to gravity,
cD is the drag coefficient, and v(t) is the velocity.
For this case, the velocity is positive even though the person is going down.
For this problem we will use metric units: the parachutist weighs 70 kilograms,
the drag coefficient is 10 kg/sec, and the gravitational acceleration is 9.8 m/sec2.
At time 0, the velocity is 0 m/sec.
Although this equation can be solved analytically, it is a good one to test with
ode45. There are two parts to solving an ODE using Matlab'sode45function:write a function that computes the right hand side of the ODE
Write a function, called
parachuteODE, that computes the derivative of v. The function should take as input the parameters t and v (in that order), and return the derivative of v using the equation above. For this problem t is not needed to compute the derivative, but in general the time is needed. It is always included in the header. The contents of yourparachuteODE.mfile should look like:function vprime = parachuteODE(t, v) g = 9.8 ; % gravity = 9.8 m/sec^2 cD = 10 ; % coef of Drag = 10 kg/sec m = 70 ; % mass = 70 kg vprime = g - (cD*v) / m;
write a script (main program) that sets up and calls
ode45The main script set the conditions that define the solution, computes the solution, and plots it.
v0 = 0; % the initial velocity t0 = 0; % the initial time tF = 20; % the end time timespan = [ t0 tF ]; % the interval (only two elements, first and last) [t_soln, v_soln] = ode45('parachuteODE', timespan, v0); % solve it! plot( t_soln, v_soln ); % plot it!Note: Even though none of the examples use the time (t) parameter to compute the derivative, it is useful to make a run in which the time value
tis printed out each timeparachuteODEis called. This will give you an idea of howode45works.You will notice that it chooses smaller time steps initially and then larger steps when the derivative is not changing rapidly. You can also see this with the command
plot(t_soln)after the call toode45.For this example, we add the problem of determining the distance that the parachutist travels while falling. We have to add another equation to account for the distance. Here is the system of ODEs:
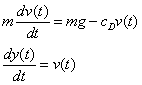
The steps you will need to do to modify your program to include this second equation are as follows:
- Change the input and output parameters in
parachuteODEto handle an input vectorw(wherewis a vector with two parts, i.e.,whas the form[v, y]) and to compute the vector of derivativeswprime. The values inwprimeshould be[vprime; yprime]where these are the derivatives of the values inw.function wprime = parachuteODE(t, w) g = 9.8 ; % gravity = 9.8 m/sec^2 cD = 10 ; % coef of Drag = 10 kg/sec m = 70 ; % mass = 70 kg v = w(1); % get v from w y = w(2); % get y from w vprime = g - (cD*v) / m; % same ODE before yprime = v; % the new ODE equation wprime = [vprime; yprime]; % the combined derivatives (must be column vector)
- Change the main program to initialize the distance (start with y(0) = 0)
and include this in the vector of initial conditions.
v0 = 0; y0 = 0; w0 = [v0 y0]; t0 = 0; tF = 20; % end time timespan = [ t0 tF ]; % only two elements, first and last [t_soln, w_soln] = ode45('parachuteODE', timespan, w0); v_soln = w_soln(:,1); y_soln = w_soln(:,2); - Change the plotting call to show both the velocity and the distance fallen.
Make sure you can identify which is which.
plot( t_soln, v_soln, 'r-', t_soln, y_soln, 'g--' );
A system with any number of ODEs can be solved by wrapping the initial values in this way and calculating each of the derivatives in the rhsode function and wrapping the result.
- Change the input and output parameters in

