Examples:

  1. Type these commands in a Maple worksheet and pay careful attention to the results of each entering each keystroke in the Maple worksheet. 
            eq1 := x^2 -> - 5*x + 6 = 0
        s1 := solve(eq1,x)
    values of x that solve eq1 are 3,2
  2. Type these commands in a Maple worksheet and pay careful attention to the results of each entering each keystroke. 
            eq2 := x^3 -> - 9*x^2 -> + 26*x - 24 = 0
        s2 := solve( eq2, x )
    values of x that solve eq2 are 2,3,4
  3. Type these commands in a Maple worksheet and pay careful attention to the results of entering each keystroke and typing the [Enter] key. 
            eq7 := x^2 -> - 17/6 -> *x - 7/3 -> = 0
        s7 := solve(eq7, x)
        s7_1 
        s7_2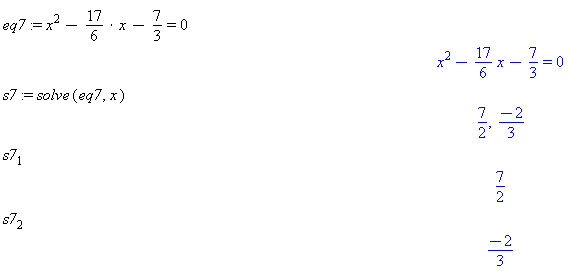
    values of x that solve eq7 are 7/2 and -3/2

    Comment: Note the underscore _ character is used to to create or access subscripted variables. Subscript 1 accesses the first solutions and so on. The square brackets [ ] can be used to do the same.

    Try s7[1] and s7[2] to compare the results. We commend using the [ ] notation to avoid some subtle issues that arise when using the subscript or underscore notation. 

  4.         eq8 := x^4 -> -313/315 -> * x^3 -> + 1/189 -> * x^2 -> + 179/945 -> * x - 2/63 -> = 0
        solve(eq8,x)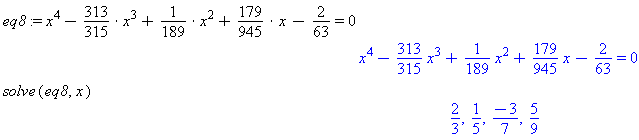
    values of x that solve eq8 are 2/3,1/5,-3/7,5/9

    Comment: Note how Maple can find the roots of very complex polynomials if the roots are rational fractions.

  5.           eq9: = a*x^3 -> + b*x^2 -> + c*x + d = 0
          solve(eq9, x)
    values of x that solve eq9 (very complex expressions)

    Comment: In this case Maple gives you the formula for the solution of a cubic equation in terms of the coefficients a, b, c, and d. 

  6.           eq10 := x^(3/2)*ln(x) - 7 = 0
          solve(eq10, x)
          fsolve(eq10, x)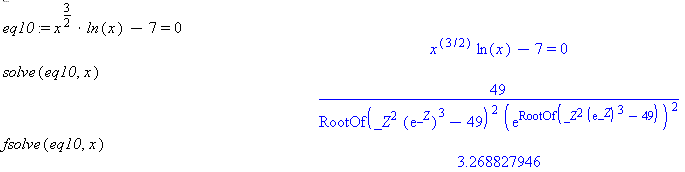
    numeric solution of eq10 is 3.268827946

    Comment: The numerical answer is returned as a decimal result because a successive approximation numerical method was used to find the solution. This would be difficult to do with paper and pencil because the computer was required to execute many iterations to get this result to such high accuracy. You should always attempt to solve equations using the Solve option or the solve command. If this does not work, then use the Solve numerically or the fsolve command.