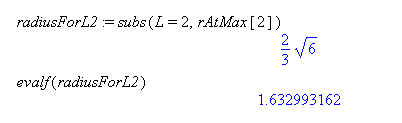Examples

  1. Find the value of the maximum volume of a cone with a slant height equal to 1

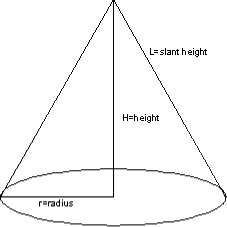
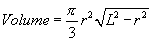
    Cone Cone Volume Formula

    Find the maximum volume of the cone above, using the formula for cone volume and L=1.

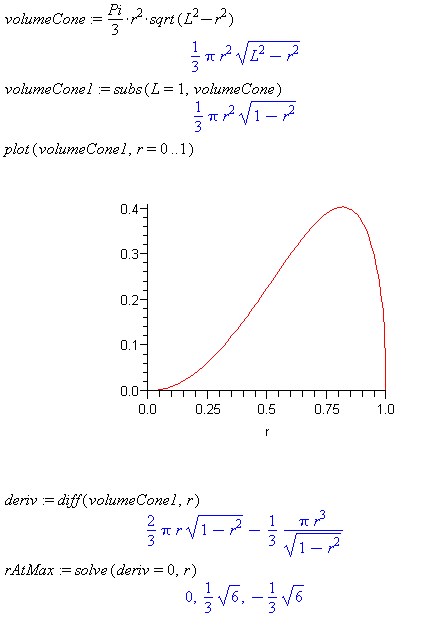
    enter, subs, diff, solve

    The positive solution is the only reasonable solution for this problem. Thus, find the max volume by substituting the third root that was found.

    Note: If you try to "solve" an expression in Maple, Maple will turn that expression into an equation by setting the expression equal to zero. Thus the last command could be replaced by: rAtmax:=solve(deriv,r) and it would still work.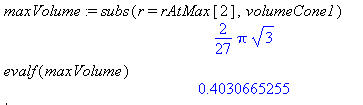

    subs and evalf

  2. Find a formula for the maximum volume of a cone in terms of its slant height

    Hint: Perform the same procedure as before but do not substitute L=1.

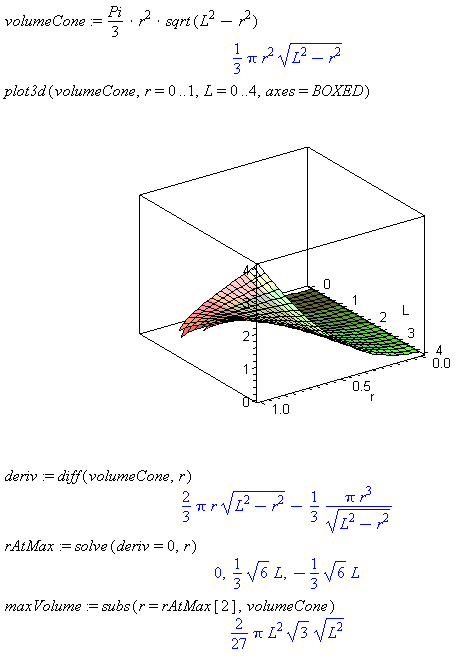
    enter, diff, solve

    Comment: Solving the problem in this way gives a formula for the result that can be used to find the max volume for any slant height. Substitute the for L to find the maxVolume.

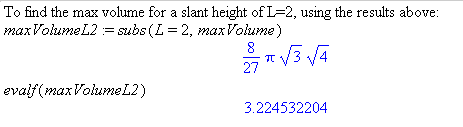
    subs, evalf

    But, what if you also need to know the radius for that slant height? First, use the formula for rAtMax to calculate the correct radius for the given slant height.

    subs, evalf