Errors and order of accuracy of numeric methods
We now look at error estimates for Euler's method. Define
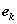 to be the error at step k. The error is the difference between the true solution of the ODE and the solution of the approximation method, that is,
to be the error at step k. The error is the difference between the true solution of the ODE and the solution of the approximation method, that is,
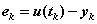 . Where
. Where
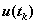 is the exact solution. Mathematicians have proven that an estimate for the error of Euler's method is the formula:
is the exact solution. Mathematicians have proven that an estimate for the error of Euler's method is the formula:
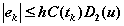
where C(t) is a function of t that depends on the behavior of F(t, y(t)), and
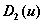 is the maximum of the second derivative of u(t) for t between
is the maximum of the second derivative of u(t) for t between
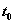 and
and
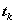 . This puts a bound on the error but does not tell us what it is.
. This puts a bound on the error but does not tell us what it is.
The significance of this estimate is that the error for Euler's method is proportional to h. That is, we expect that if we reduce h by 1/2 then
the error in the approximate solution will be reduced by about 1/2. We can test this using our simple ODE where we know the exact solution. We
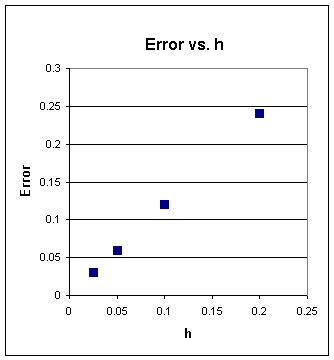
evaluate the approximate solution for different values of h. The results are shown in the table below. We see that each reduction of h by 1/2
indeed results in a reduction of the error at
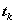 =2.2 of 1/2.
=2.2 of 1/2.
| h |
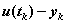
|
|---|---|
| 0.2 | 0.24 |
| 0.1 | 0.12 |
| 0.05 | 0.06 |
| 0.025 | 0.03 |
The following figure emphasizes the point that the error is reduced in direct proportion to the reduction of h.
It is in fact quite inefficient to reduce the error by reducing the value of h using a first order accurate method. In practice, this is never
done. Instead we use higher order accurate methods. In general, the error of an n-th order Runge-Kutta method is said to be
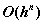 . This is called n-th order accuracy, so that Euler's method has first-order accuracy. These higher order methods require more work to estimate the derivative on each time step, but in return they have the property that the error is reduced by a power of h as h is reduced. Thus a fourth order method reduces the error by 1/16 when h is reduced by 1/2.
. This is called n-th order accuracy, so that Euler's method has first-order accuracy. These higher order methods require more work to estimate the derivative on each time step, but in return they have the property that the error is reduced by a power of h as h is reduced. Thus a fourth order method reduces the error by 1/16 when h is reduced by 1/2.
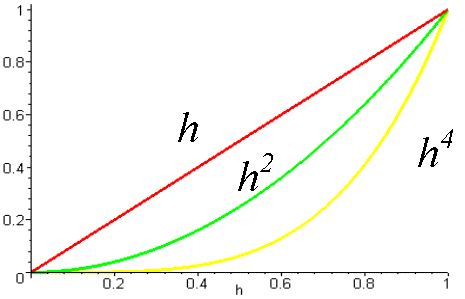
This is demonstrated schematically in the figure below. We see that as h is reduced, the error of the first order method labeled 'h' is reduced linearly. However the errors of the higher order methods are reduced significantly more for the same amount of reduction in h. This greatly improves the efficiency of the method for computing accurate approximations to the solution.
The Runge-Kutta method is also discussed in the Successive Numeric Approximation module.

