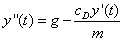Exercises

Use the code presented in the ode45 Examples section to answer each of these questions.

1. How far will the parachutist fall in 20 seconds?

   The distance the parachutist has fallen in 20 seconds is the last value of the y_soln vector of Example 2.

   % How far will the parachutist fall in 20 seconds?
   time20 = length(t_soln);  % the last value in t is 20, time20 is the index
                        % of the last value
   disp(['The last time value is: ', num2str(t_soln(time20))]) % just checking
   disp(['In 20 seconds the parachutists falls ', num2str(y_soln(time20)), ...
         ' m'])

   The output is:

   The last time value is: 20
   In 20 seconds the parachutists falls 919.3792 m
   

2. How fast is the parachutist falling after 20 seconds?

   The velocity of the parachutist at 20 seconds is the last value of the v_soln of Example 2.

   % How fast is he falling after 20 seconds?
   disp(['After 20 seconds the parachutists is falling ', ...
         num2str(v_soln(time20)), ' m/sec'])

   The output is:

   After 20 seconds the parachutists is falling 64.6601 m/sec

3. From the plot of the velocity, it is apparent that there is a limiting velocity. What is the value of this terminal velocity?

   % Setting v'(t) = 0 and solving for v(t) we get that the steady-state
   % value is v(t) = g*m/cD
   terminalV = g*m/cD;
   disp(['The terminal velocity is ', num2str(terminalV), ' m/sec'])

   The output is:

   The terminal velocity is 68.6 m/sec

4. Write this system of ordinary differential equations as a single second-order differential equation for y(t).

   Since y'(t) = v(t), taking the derivative of each side we get y''(t) = v'(t). So, we can rewrite the system of ODEs as the following second-order ODE: