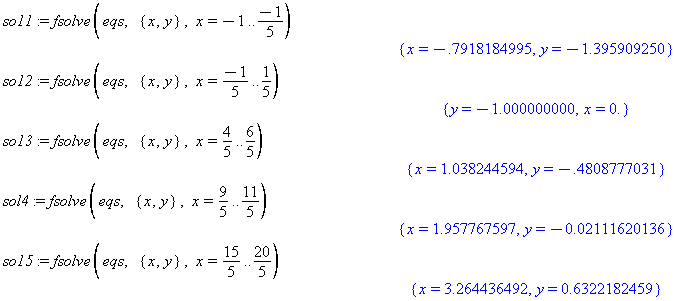Examples
expr1 := cos(2*theta)-cos(theta)
plot(expr1, theta=0..2*Pi)
solve(expr1=0,theta)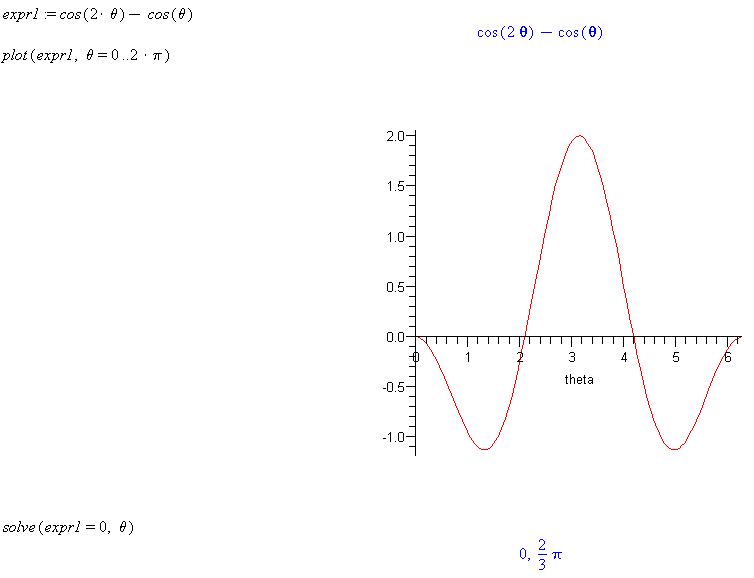
Comment: The solve command returns two values. From the plot you can see that the expression is symmetric about
 . Thus other solutions are 4
. Thus other solutions are 4
 /3 and 2
/3 and 2
 .
.
expr2 := sin(3*theta)-cos(theta)
plot(expr2, theta = -Pi..Pi)
sol := solve(expr2=0,theta)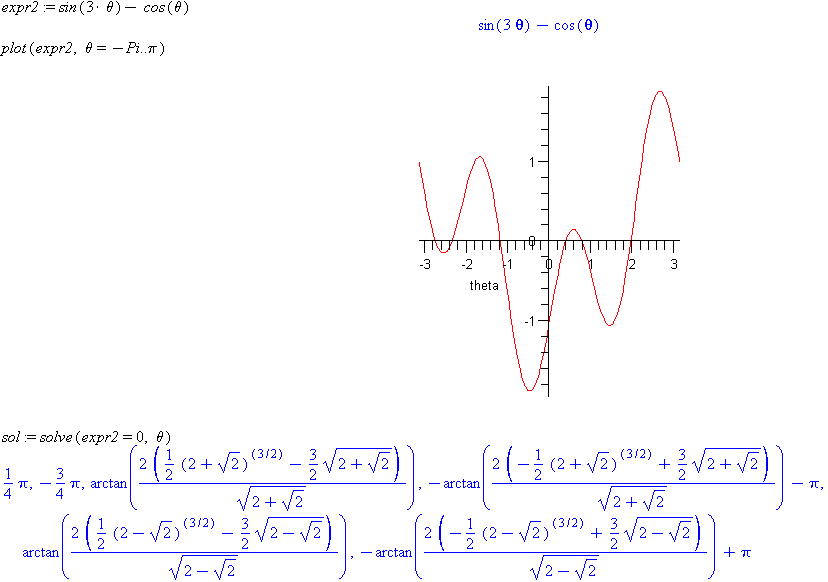
Comment: Six roots are returned by the solve command. Two solutions are nice, each a multiple of
 and differing by
and differing by
 . The other four roots contain
. The other four roots contain arctanfunctions. Simplify the other four roots. The roots are a list and can be referenced assol[1], sol[2], sol[3]…sol[6].Apply the commandsimplify(sol[3]). Apply this to the other complicated roots. Now you can note that the only unique roots are /8,
/8,
 /4, and 5
/4, and 5
 /8. The other three are the next in the sequence, all shifted by integer multiples of
/8. The other three are the next in the sequence, all shifted by integer multiples of
 . In this case Maple found redundant roots. So Maple is powerful, but is not a substitute for
understanding math.
. In this case Maple found redundant roots. So Maple is powerful, but is not a substitute for
understanding math.
![simplify(sol[1])](example2b.gif)
eq31 := y=1/2*x-1
eq32 := y=sin(3*x)-cos(x)
exprs := rhs(eq31), rhs(eq32)
plot( {exprs}, x=-10..10)
sol := solve([eq31, eq32], [x, y])
solall := allvalues(sol)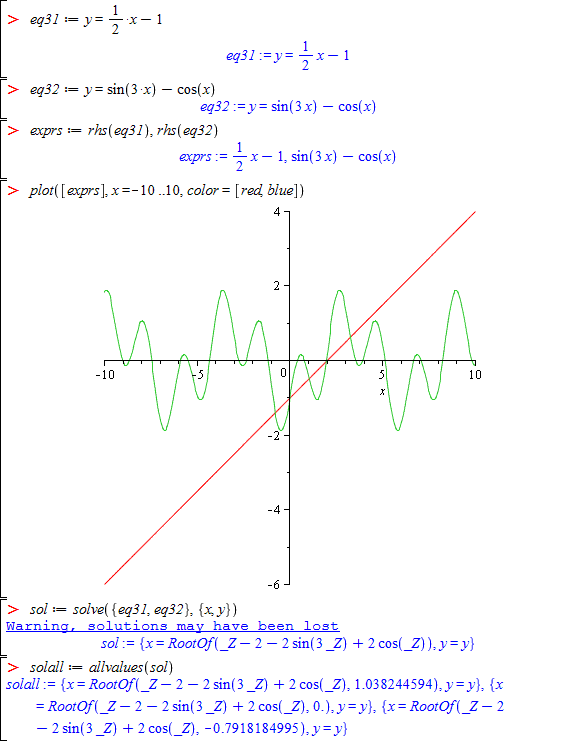
Comment: The
solvecommand fails. So thefsolvecommand must be used for each of the five roots. Go on to the next example to see the roots.sol1 := fsolve(eqs, {x,y}, x=-1..-1/5)
sol2 := fsolve(eqs, {x,y}, x=-1/5..1/5)
sol3 := fsolve(eqs, {x,y}, x=4/5..6/5)
sol4 := fsolve(eqs, {x,y}, x=9/5..11/5)
sol5 := fsolve(eqs, {x,y}, x=15/5..20/5)