Exercises

1. Solve the ODE: 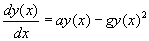with a=5 and g=0.1. However, solve the ODE with the intial condition y(0)=100 and then solve with the initial condition y(0)=10. Then plot both solutions on an appropriate time scale(x) to see the steady state behavior of both solutions on the same plot.

   The following are two possible ways to do this problem, there are MANY other ways to do this problem:
   
   METHOD 1 (All commands)
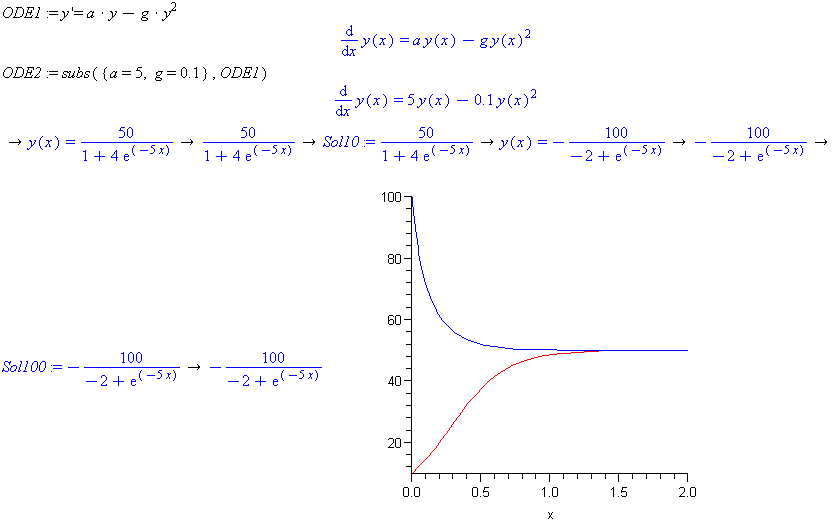
   ODE1:= y'a*y-g*y^2
ODE2:=subs({a=5, g=0.1}, ODE1)
sol1:=dsolve([ODE2, y(0)=100], y(x))
sol2:=dsolve([ODE2, y(0)=10], y(x))
plot([rhs(sol1), rhs(sol2)], x=0..2)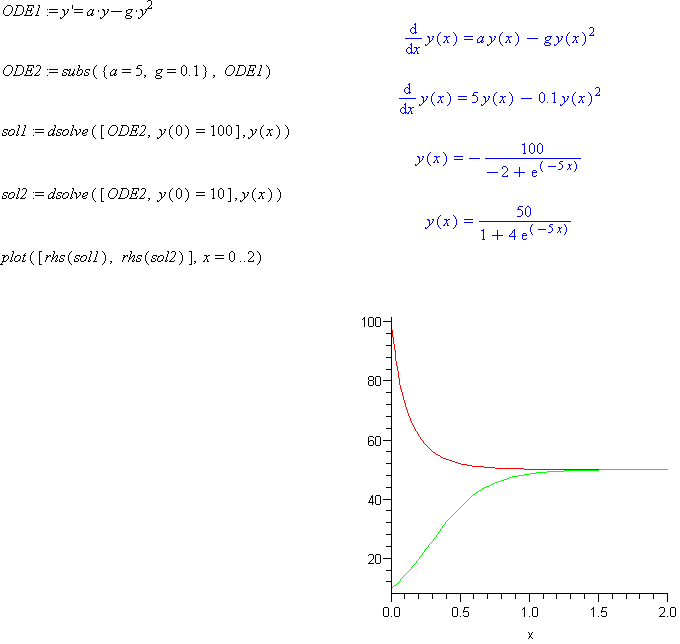

   
   
   

   METHOD 2 (DE interactive)
   ODE1:=y'=a*y-g*y^2
ODE2:=subs({a=5, g=0.1}, ODE1)
Right click-> Solve DE interactively
   Click->Conditions-> Edit-> y at 0 = 100 ->Add -> Done
   Click-> Solve Symbolically
   Click-> Solve
   Change bottom left of window to read: "On Quit, Return Solution"
   Click-> Quit
   Right click on solution -> Right hand-side
   Right click-> Assign to a Name: Sol100
   Repeat the steps from Solve DE interactively down but use the condition y at 0 =10 and in the last step give the name Sol10
   Open Plot Builder
   Add Sol10 and Sol100
   Click Done and select 2-D plot from 0 to 2