CS/ECE 252 Introduction to Computer Engineering Spring 2009 All Sections Instructor David A. Wood TAs Mengmeng Chen, Maheswaran Venkatachalam & Daniel Wong URL: http://www.cs.wisc.edu/~david/courses/cs252/Spring2009/

Homework 3 // Due at lecture Feb 23, Mon

Primary contact for this homework: Mengmeng Chen [mchen at cs dot wisc dot edu]

You must do this homework alone. Please staple multiple pages together.

Problem 1

Draw a logic circuit corresponding to the following logic expression. You must use four NOT gates, three 2-input OR gates and two 2-input AND gates.

NOT((NOT(A) OR B) AND (C OR NOT(B))) AND (NOT(D) OR A)

Problem 2

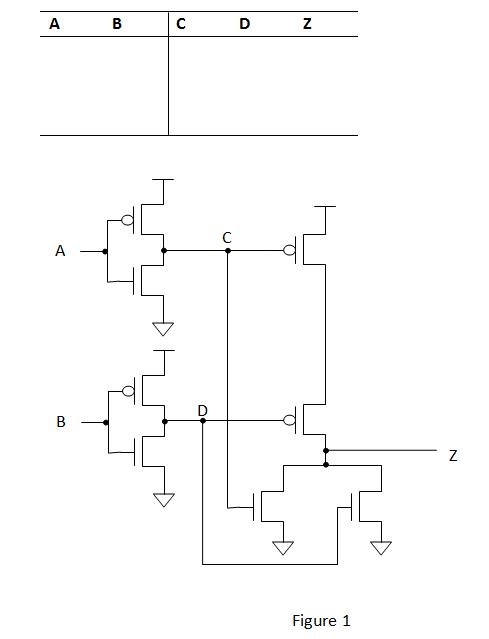
For the transistor-level circuit in Figure 1, fill in the truth table. What is Z in terms of A and B?

Problem 3

Fill in the truth table for the logical expression NOT(A) AND NOT(A OR B).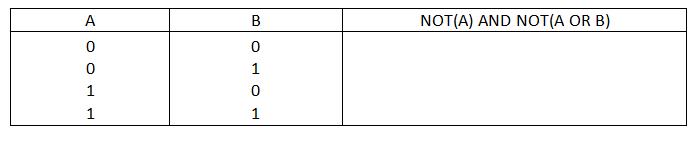

Problem 4

For this question, refer to the figure below.

1. Describe the output of this logic circuit when the select line S is a logical 0. That is, what is the output Z for each value of A?
2. If the select line S is switched from a logical 0 to 1, what will the output be?
3. Is this logic circuit a storage element? Explain why or why not.

Problem 5

How many different memory locations can we have with 32-bit address? If the memory is byte-addressable, how many bits does the memory hold?

Problem 6

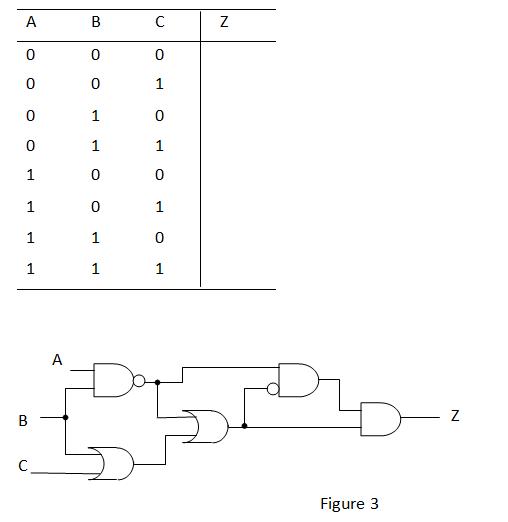
Given the logic circuit in Figure 3, fill in the truth table for the output value Z.

Problem 7

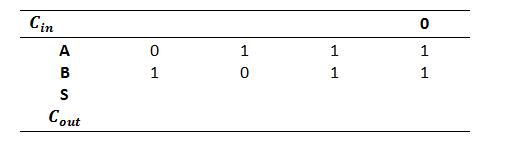
A full binary adder, described in Figures 3.14 and 3.15 on page 62 of the book, adds three inputs A, B, and Cin and produces two outputs, the sum S and the carry out Cout. These can be combined into a four-bit binary adder as shown in Figure 3.16 on page 63. If A and B are four-bit unsigned binary numbers, 0111 and 1011, complete the table below for each of the sum and carry bits. Check your answer by adding the decimal values of A and B and comparing the sum with S. Are the answers the same? Why or Why not?

Problem 8

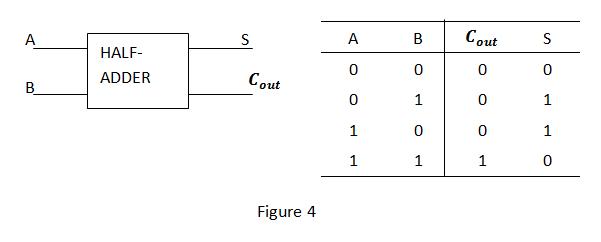
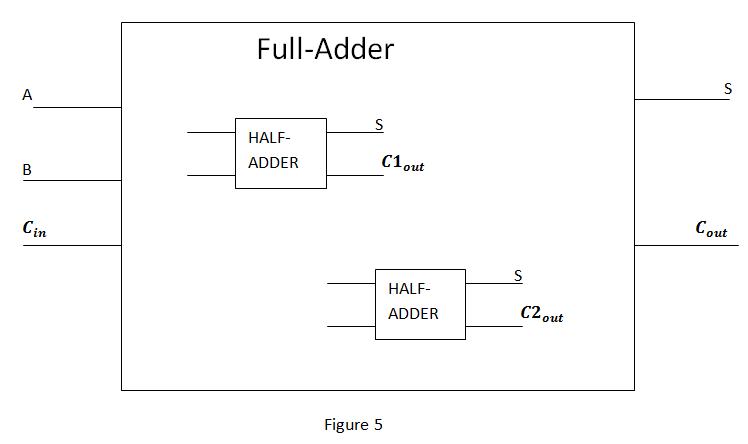
A half-adder is another kind of logic circuit that can perform binary addition. The difference between a full-adder and a half-adder is that a half-adder does not take the carry-in as input. A typical half-adder is illustrated in Figure 4. One way to build a full-adder is to use two half-adders as basic building blocks. Now try to build a full-adder by drawing the necessary connections in Figure 5. (Note that you need one more 2-input gate (‘AND’ or ‘OR’) to finish the job. Feel free to choose one and add it in the box.)