CS/ECE 552 Introduction to Computer Architecture Spring 2010 Section 1 Instructor David A. Wood and T. A. Tony Nowatzki URL: http://www.cs.wisc.edu/~david/courses/cs552/S10/

CS/ECE 552 : Introduction to Computer Architecture
Spring 2010
Prof. Wood
Problem Set #6

Due: April 30th, 2010

Assignment is to be done individually

20 points each

1.  Problem 1

Please read the Error Correcting Codes handout for help with this problem.

Consider the example single-error-correcting code with a minimum Hamming distance of three example in the ECC1 handout.

Use this code for the following questions:

1. Find the codewords for these datawords :

   1. 00000010

   2. 10101000

   3. 01100110

   4. 11011011

2. For this part assume that at most one bit can be in error. If the following values are read from the memory (stored using the above encoding in the order C3 C2 C1 C0 b7 b6 b5 b4 b3 b2 b1 b0), find the correct dataword.

   1. 0000 00000111

   2. 1011 10000111

   3. 0010 10101001

   4. 0111 11001010

2.  Problem 2 (instructions updated April 21)

Multiply the following 2's complement 8-bit numbers using Booth's algorithm. Show your work in detail. Verify your answer by computing A, B and the product in decimal.

Multiplicand A = 1101 0101 Multiplier B = 0101 0101

3.  Problem 3

Divide the following positive numbers using the restoring division algorithm. Show all the steps as in Figure 3.11 on page 240 of the COD4e text book.

Verify your answer by converting A and B and your result (A / B) and remainder to decimal.

A = 0110 1101 B = 0110

4.  Problem 4

1. Show the IEEE 754 binary representation for the floating point number 343.723 (base 10)

2. Convert the following number given in IEEE 754 binary representation to the equivalent decimal number
   1100 0000 1100 0100 1001 0000 0000 0000

5.  Problem 5

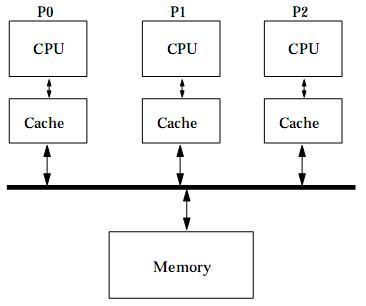
Symmetric Multiprocessors (SMPs) are the most common computer systems that use multiple processors.

Most SMPs use a shared bus to connect the processors to a (logically) shared memory, as illustrated

above. Each processor has one or more writeback caches to reduce both memory latency and

contention for the shared bus. A write-invalidate cache coherence protocol is used to ensure that caches

maintain a coherent view of the memory state.

Assume a three-state write-invalidate protocol, as discussed in class and in the textbook. The three

states are:

Modified (M), also known as Read/Write (Dirty)

Shared (S), also known as Read Only (Clean)

Invalid (I)

Consider an SMP with the initial memory state as shown on the next page. For simplicity, the table

shows only the memory block at address 100 and the block only contains one word. Consider a

sequence of processor operations (time flows down the page). For each processor operation, write a one

or two sentence description of the actions taken by the coherence protocol (I have completed the first

one for you, as an example). Fill in the tables with the state of the caches and memory (for block 100)

after each operation has completed.

Recall that $0 in MIPS always contains the value zero.