CS839 - Foundation Models
Multimodal Geometry of Truth
Abstract
Building on “The Geometry of Truth” paper, we extend the research using various models, ranging from small ones the recent LLaMA 3.3-70B, to explore truth representations across different modalities. Our experimental results indicate that linear structure does not necessarily emerge in all truth statements, for instance in mathematical problems of diverse types. Key contributions include leveraging state-of-the-art multimodal models, comparing their performances, and introducing two new datasets designed for image and mathematical reasoning tasks. These findings suggest that advancements in model architecture and scale play a critical role in capturing cross-modal truth representations. The potential experimental results provide insights into the universal geometric structures underlying truth-related representations and their implications for advancing multi-modal reasoning.
Introduction and method
Large Language Models (LLMs) have demonstrated remarkable capabilities in natural language understanding, generation, and reasoning [2]. Among these developments, the paper The Geometry of Truth [1] explored the latent space of LLMs, revealing an intriguing phenomenon: truth and falsehood in text-based datasets can be represented as distinct, linearly separable regions in the latent space. This geometric property of latent representations provides new insights into how LLMs internally encode the veracity of information, offering a basis for interpretability and trustworthiness in artificial intelligence systems.
However, while these findings are compelling for text-based tasks, the generalizability of such geometric structures across other domains remains an open question. Understanding whether similar truth-related latent structures exist in mathematical reasoning and multi-modal tasks (e.g., image-text pairs) is critical for the development of versatile and reliable AI systems. For instance, in mathematical reasoning, where models often rely on techniques like chain-of-thought (CoT) prompting [3] or tree-of-thought reasoning [4], the ability to encode truth as a linearly separable property could enable models to autonomously verify the correctness of intermediate steps. In multi-modal contexts, such as image-text alignment tasks, the ability to distinguish between true and false visual claims could significantly improve applications in misinformation detection, automated content moderation, and forensic image analysis.
Motivated by these possibilities, this project extends the findings of [1] by investigating whether the linear separability of truth-related representations generalizes to two additional modalities: mathematical reasoning and multi-modal tasks. Specifically, we leverage the LLaMA 3 family of models, which supports multi-modal capabilities, allowing us to explore truth-related latent structures in both image-text pairs and mathematical statements. So unlike the original study, which focused exclusively on text-based datasets using LLaMA 2, our work introduces new datasets and tasks designed to evaluate the linear separability of truth and falsehood across modalities.
Our approach builds upon the methodologies outlined in The Geometry of Truth, while introducing several key modifications: (1) Mathematical Reasoning: We curate datasets consisting of mathematical statements with clear truth values. Using LLaMA 3, we extract latent representations for these statements and evaluate their linear separability using techniques such as linear classifiers (e.g., SVMs) and visualization methods like PCA. (2) Multi-modal Tasks: For image-text pairs, we create a dataset of images paired with descriptive statements, incorporating diverse and challenging scenarios. LLaMA 3’s multi-modal capability enables the extraction of joint latent representations for these pairs, which we analyze for linear separability. (3) Evaluation Metrics: Following the original paper, we evaluate the separability of true and false representations using classification accuracy, dimensionality reduction techniques, and cross-domain comparisons.
By extending the analysis of truth-related representations to mathematical reasoning and multi-modal tasks, the potential outcomes of this project could have far-reaching implications. If truth-related representations are universally linearly separable across modalities, this could enable models to autonomously verify intermediate reasoning steps in mathematical problems or identify falsehoods in multi-modal data. Such advancements would represent a significant step forward in the development of interpretable and reliable AI systems.
Related Work
Linear Representations in LLMs.
A substantial body of research has investigated whether LLMs encode structured world models in their latent spaces. Early work analyzed individual neurons’ roles [5] and later extended these ideas to linear combinations of neurons, which encode more abstract concepts. The Geometry of Truth [1] provide evidence that truth and falsehood are captured as linearly separable features in sufficiently large LLMs. Their work demonstrates that such representations emerge with model scale and are causally implicated in model outputs, a finding that complements studies on the generalization capabilities of linear probes.
Truthfulness and Probing.
Several recent studies have explored methods for probing the truthfulness of LLMs. Logistic regression-based probes have been widely adopted [1], [2], [6], but their generalization ability often suffers in complex contexts, such as negated statements. Contrastive techniques, such as contrast-consistent search (CCS), have also been proposed to improve generalization by leveraging contrast pairs of true/false statements. However, these methods face challenges in disentangling features that merely correlate with truth from those that causally encode it. This line of research is critical in addressing the limitations of LLMs when tasked with factual reasoning.
Causal Interventions and Truth Representation.
Beyond probing, causal intervention techniques have been applied to LLM representations to assess their encoding of specific concepts. Recent work [1] has shown that intervening on hidden states identified as encoding truth can systematically alter model outputs, providing evidence of causal representation. This aligns with broader research on causal interpretability in neural networks, such as [7], [8].
Reasoning via Internal Representations.
Reasoning capabilities in LLMs have been explored extensively through prompting strategies, such as chain-of-thought prompting [3] and tree-of-thought reasoning [4]. These methods demonstrate that reasoning chains can be elicited by providing structured prompts, suggesting the presence of latent reasoning abilities. However, the underlying representations enabling such reasoning—whether they align with truth representations or function orthogonally—remain an open question, partially addressed by studies like [1].
Curated Datasets
The quality and structure of the dataset play a critical role in understanding how LLMs represent truth and falsehood. To facilitate our analysis, we propose two distinct true/false datasets:
-
Sythetic Math Datasets
We curated specialized mathematical datasets to evaluate models’ basic arithmetic capabilities. Each dataset contains 500 statements with binary truth values (true/false) and focuses on fundamental mathematical operations. The datasets are structured as follows:
- Multiplication: x multiply by y is z.
- Division: x divided by y is z.
- Square root: The square root of x is y.
- Power: x to the power of y is z.
- Simple Algebra: If \(a_1x + b_1y + c_1 = z_1\), and \(a_2x + b_2y + c_2 = z_2\), then \(x = k\).
We extended the original paper’s scope from simple numerical comparisons (e.g., x > y) to a broader range of arithmetic operations. This expansion allows us to test whether the paper’s findings generalizes to other foundational mathematical tasks. By incorporating operations such as multiplication, division, square roots, and basic algebra, we assess if the patterns observed in numerical comparison tasks persist across different types of mathematical reasoning.
-
Multimodal Dataset
Image captioning is a very famous task in computer vision area - the input is an image, and the output is a text description. Therefore, we collect 1K image-text pairs from the TextCaps [9] dataset as True statements. And we simply exchange the order of texts so that we can get the mismatched image-text pairs as the False statements. The structure illustration is shown as below:

Experiments
Setting
We extend the original work in two directions: (a) evaluating a broader range of language models, and (b) testing on new datasets. Our model selection spans both large and small architectures to investigate how model scale affects geometric properties of truth representation. For larger models, we experiment with Llama3-13B and 70B, while for smaller models, we evaluate Qwen2-1.5B and TinyLlama-1.1B-Chat-v1.0. All models are accessed through the HuggingFace platform using their default configurations.
Experiments on small models
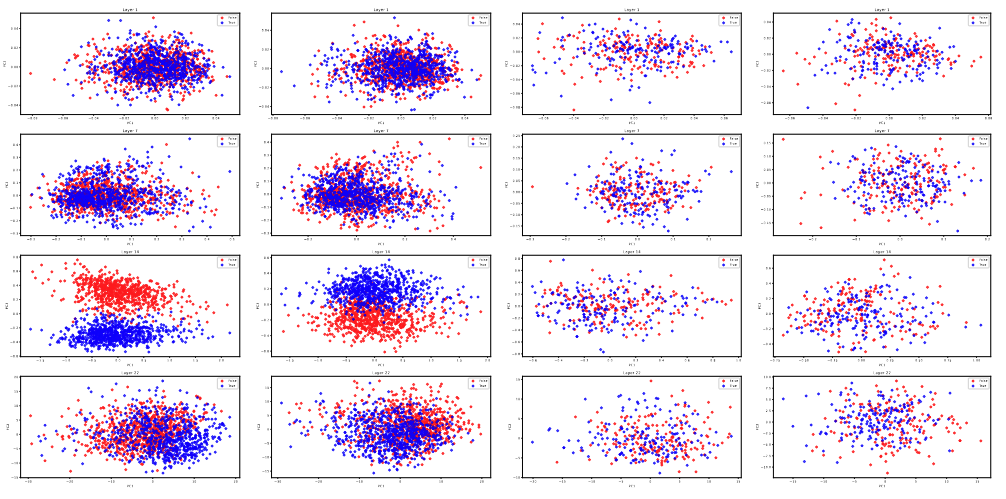
Our analysis of Qwen2-1.5B and TinyLlama-1.1B-Chat-v1.0 reveals that truth values are generally not linearly separable in their hidden representations across most layers. The notable exception is layer 14 of TinyLlama, which exhibits clear geometric separation between true and false statements. This finding suggests that the capacity to develop linearly separable truth representations may not be uniformly distributed across model architectures or layer depths.
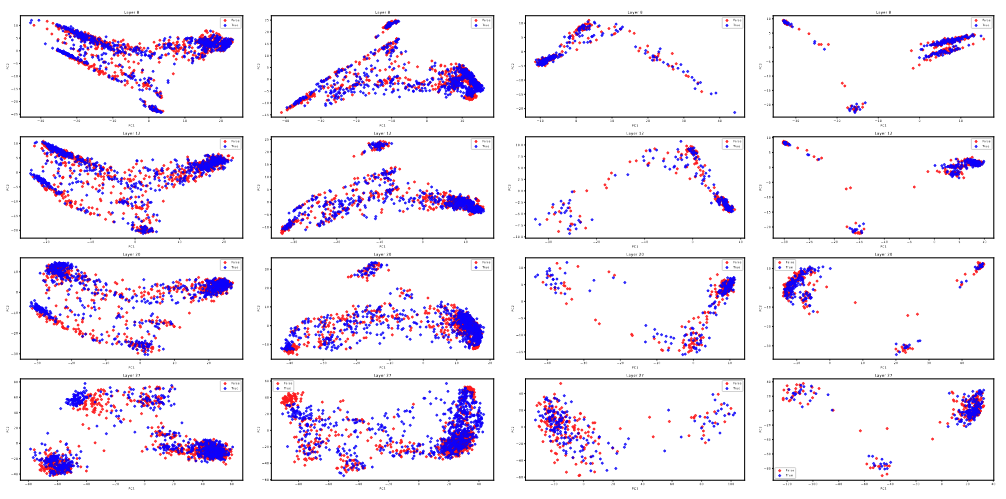
Experiments on math datasets using Llama 3.2-13B
As shown in the Fig. 4 below, the results obtained from using the LLaMA 3-13B model on the mathematical dataset reveal significant differences in the linear separability of truth-related representations across various mathematical operations: 1.Algebra Operations: The data exhibits a certain degree of linear separability, where the red (true) and blue (false) points are distributed in different regions of the latent space. However, the boundary is not entirely distinct. 2. Square Root Operations: The data points are more intermixed, with weaker linear separability between true and false values. 3. Multiplication Operations: Strong linear separability is observed, with red and blue points showing clear separation trends. 4. Power Operations: The data distribution is more complex, and the true and false values overlap significantly, indicating poor linear separability. 5. Division Operations: The data demonstrates good linear separability, with red and blue points clearly distinguished.
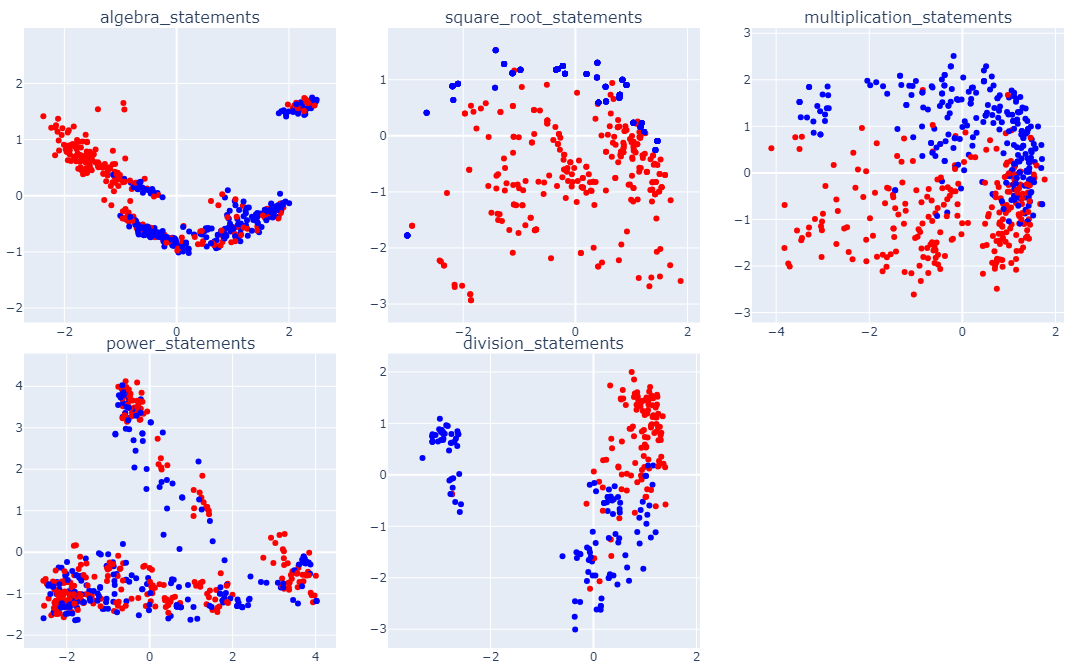
These results suggest that the model’s ability to encode truth-related geometric structures in the latent space varies across different types of mathematical operations. For some operations, such as multiplication and division, the model captures well-separated structures, while for others, such as square root and power operations, the separability is weaker or absent. These differences may be influenced by the complexity of the operations, data distribution characteristics, or limitations of the model architecture, warranting further investigation.
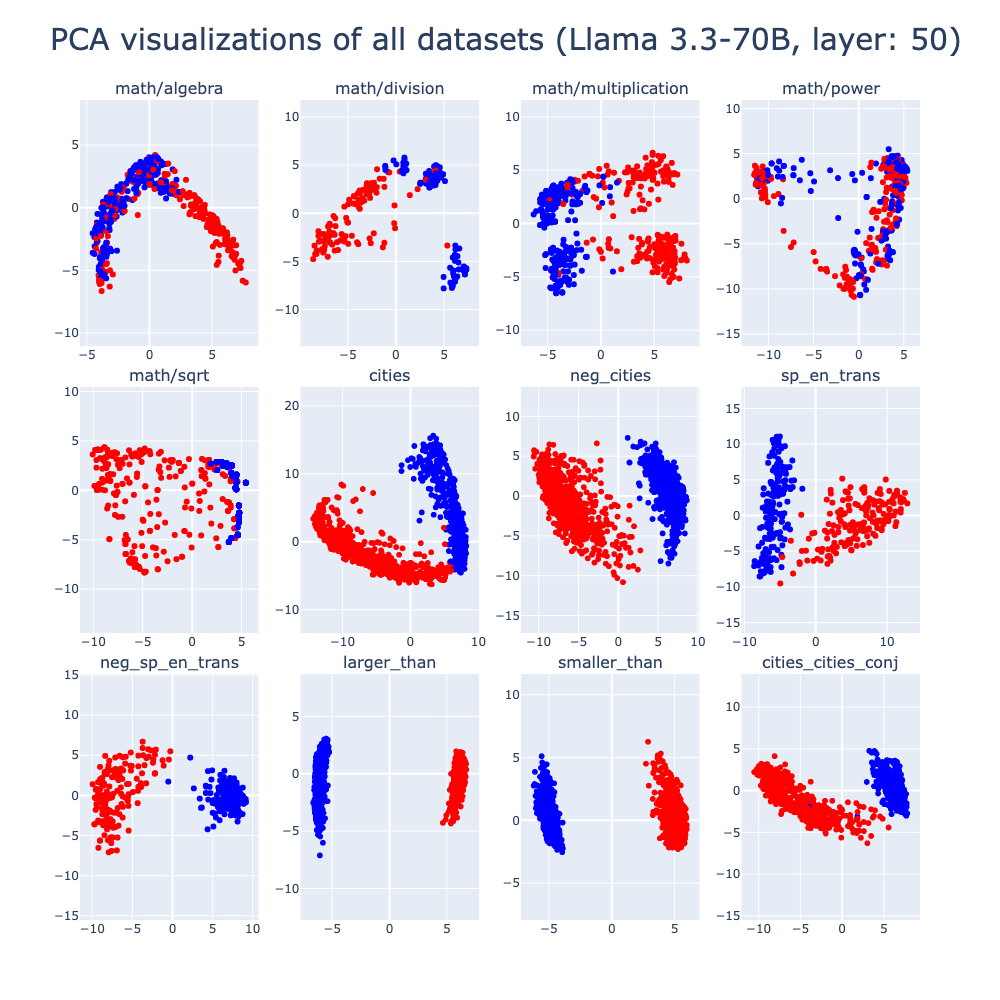
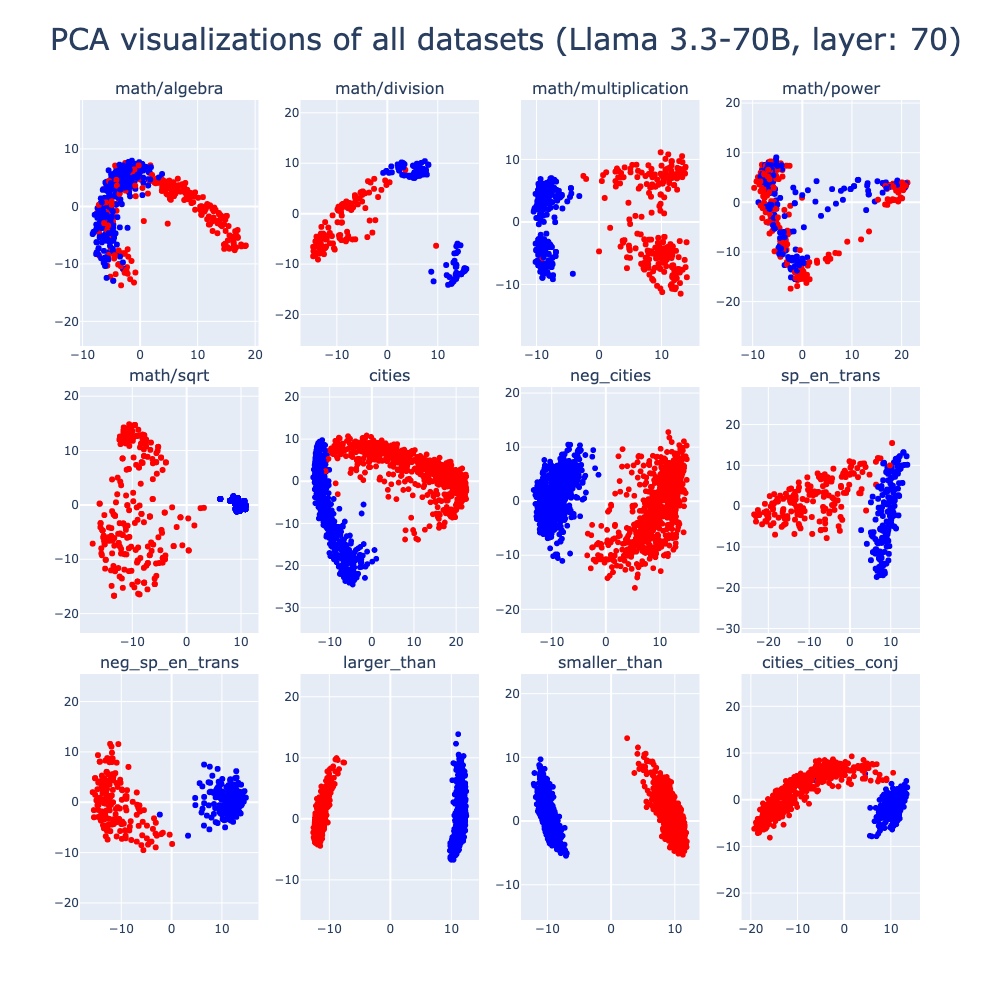
Note for section 4.2 and 4.3: Since the results when we use the Llama3-70B will not change our conclusions (but we can see better geometry separation), we show the results on cities, trans and math datasets in the Appendix. Please check section 6 for details.
Experiments on Multimodal Dataset using Llama3
For multimodal experiments, we encountered challenges with the use of the NNsight https://nnsight.net/ library in Python, which is employed for the activation patching and extraction steps. The official library is not natively designed to support multimodal data, requiring modifications to adapt it for our needs. While we began implementing these changes, we were unable to complete the experiments due to these technical limitations. We put special emphasis on testing the truth encoding for a variety of datasets representing different types of mathematical structures and formats, such as equations and arithmetic.
Conclusion and Future Work
This project extends “The Geometry of Truth” by exploring the linear separability of truth-related representations in mathematical reasoning and multimodal tasks. Results show that separability varies across tasks: while operations like multiplication and division exhibit strong separability, others like square root and power do not. Similarly, multimodal tasks show inconsistent separability, highlighting challenges in generalizing truth representations across modalities. These findings suggest that the complexity of tasks and the inherent structure of the data significantly influence the ability of models to encode truth-related representations, underscoring the need for further investigation into model architecture and dataset design.
Therefore, two key areas remain open for further exploration:
-
Advancing Models, Visualizations, and Datasets: Since our findings reveal that truth-related representations are not always linearly separable, it remains unclear whether this is due to limitations in the visualization techniques, the complexity of the datasets, or inherent challenges in the models themselves. Future work should investigate these possibilities by improving visualization methods, refining model architectures, and designing enhanced datasets. Experiments on richer logical structures and domain-specific factual claims will help determine whether these advancements can better capture and generalize truth representations across diverse tasks and modalities.
-
Applications in Model Alignment: While our work demonstrates that truth representations exhibit varying degrees of separability in LLM outputs, leveraging these findings to improve model alignment remains an open challenge. Specifically, future research could explore how these representations—whether linearly separable or not—can be utilized to reduce hallucinations and improve factual accuracy in model-generated content. For example, methods like truth-specific fine-tuning or reinforcement learning could be adapted to account for non-linear truth structures, enhancing both factual consistency and interpretability in diverse tasks and modalities.
Appendix

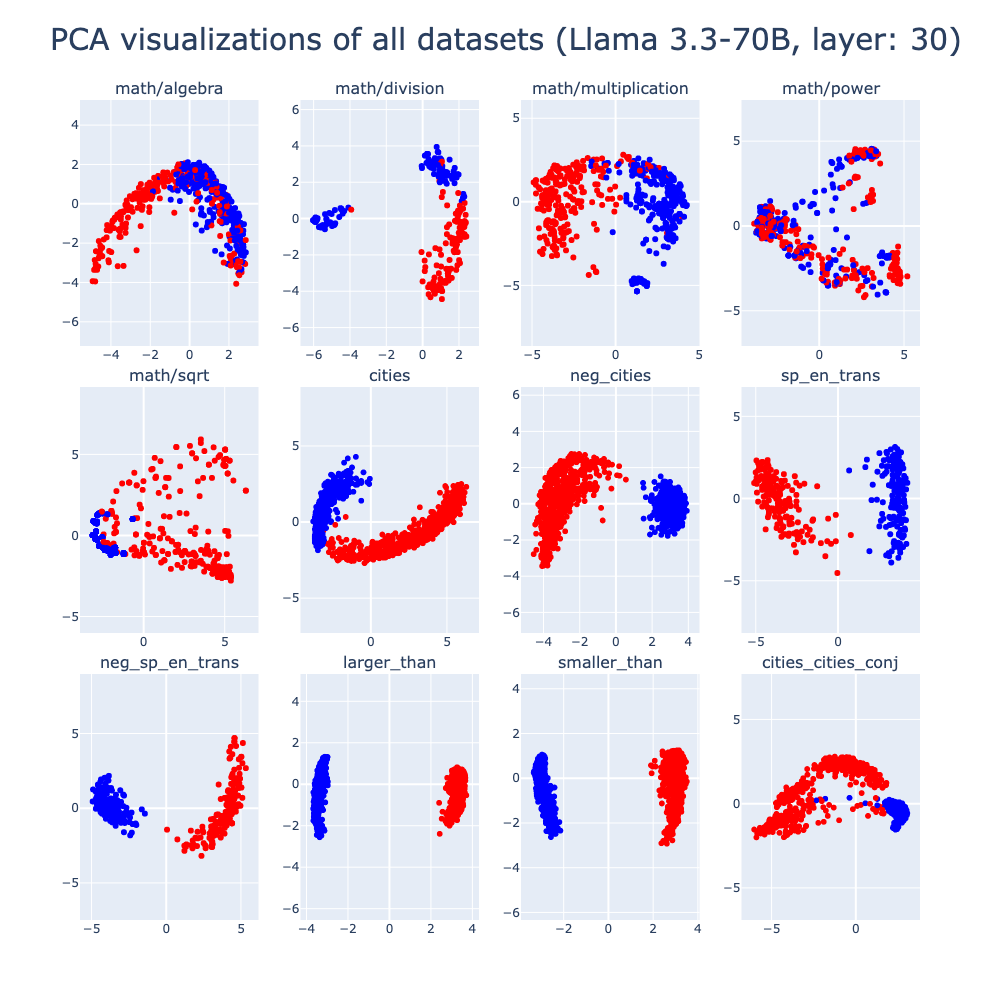
References
- The Geometry of Truth: Emergent Linear Structure in Large Language Model Representations of True/False Datasets, Marks et. al., COLM 2024
- GPT-4 Technical Report, OpenAI 2024
- Chain-of-Thought Prompting Elicits Reasoning in Large Language Models, Wei et. al. NeurIPS 2022
- Tree of Thoughts: Deliberate Problem Solving with Large Language Models, Yao et. al. NeurIPS 2023
- Understanding the role of individual units in a deep neural network, Bau et. al. PNAS 2020
- Understanding intermediate layers using linear classifier probes, Alain et. al. ICLR 2027 Workshop track
- Causal Analysis for Robust Interpretability of Neural Networks, Ahmad et. al. IEEE/CVF 2024
- Causal Abstractions of Neural Networks, Geiger et. al. 2021
- TextCaps: a Dataset for Image Captioning with Reading Comprehension, Sidorov et. al. 2020