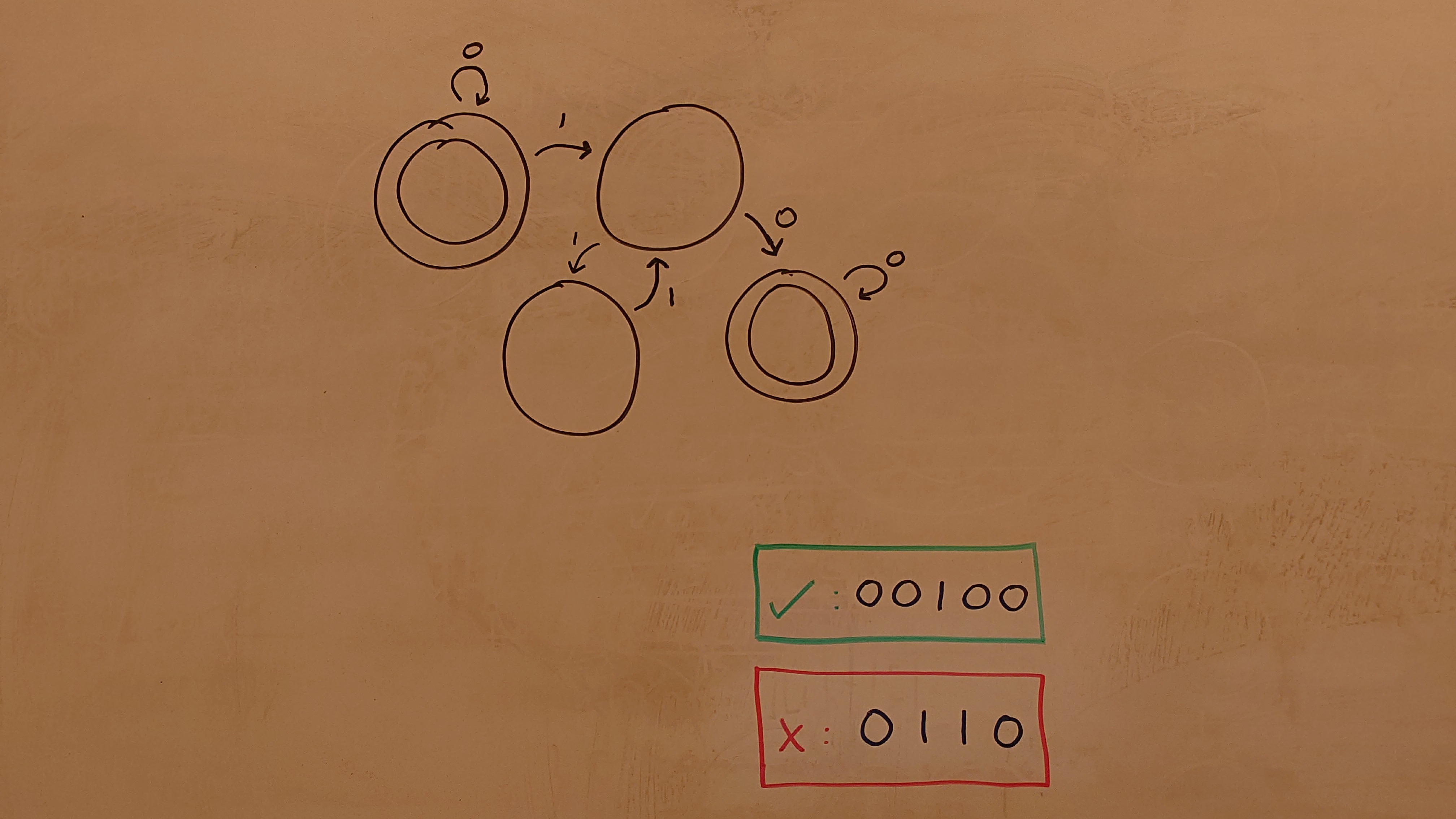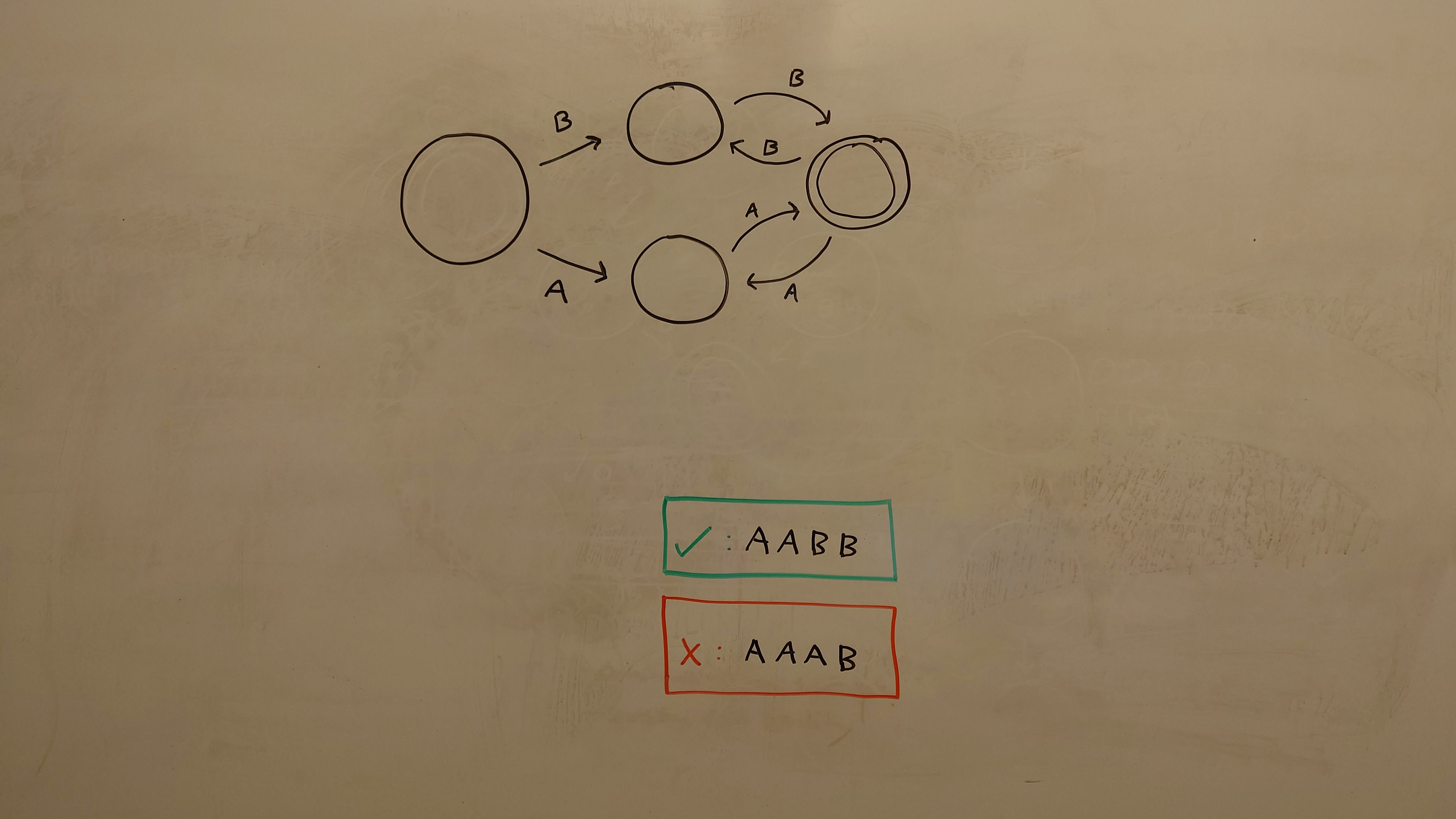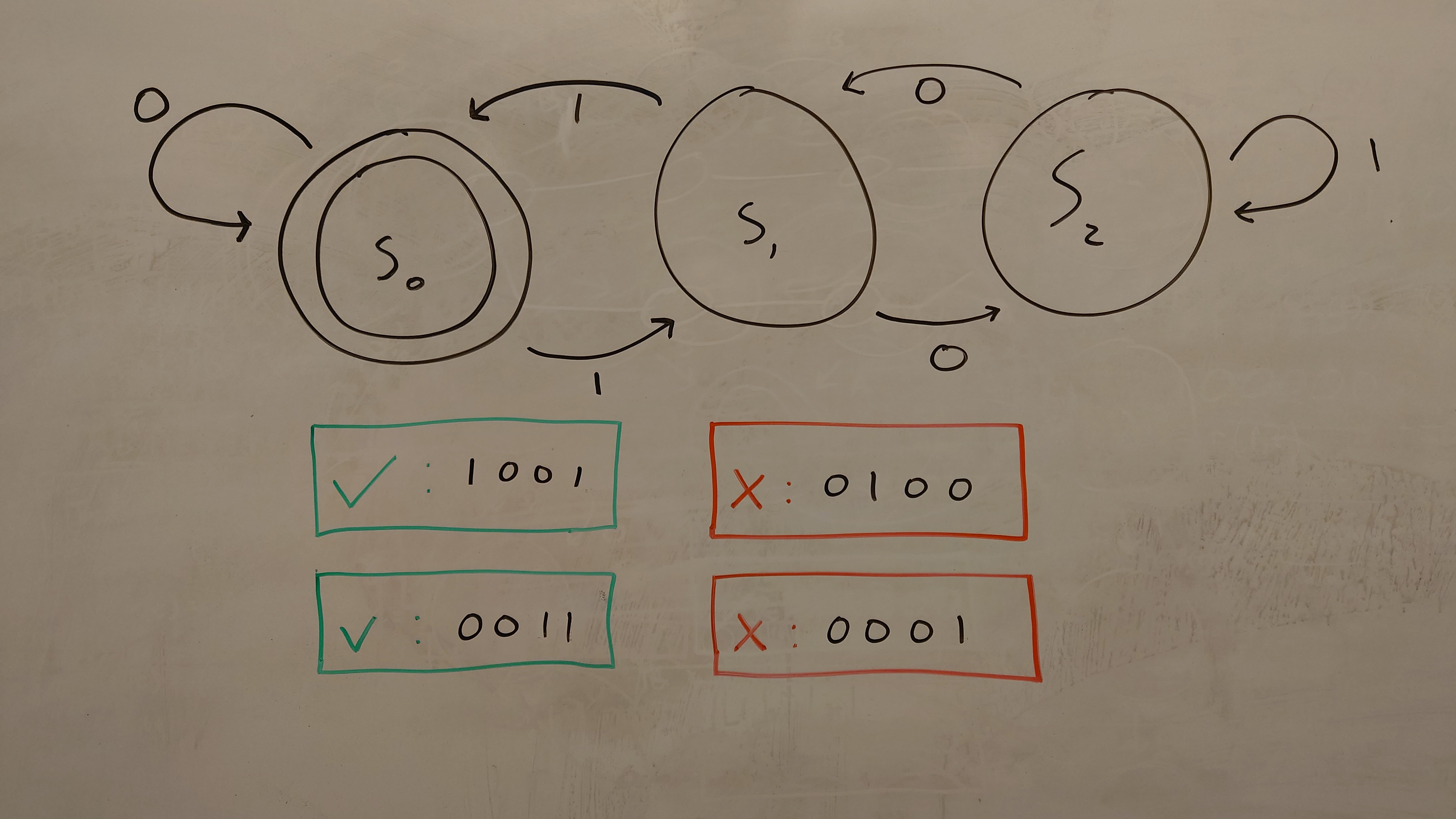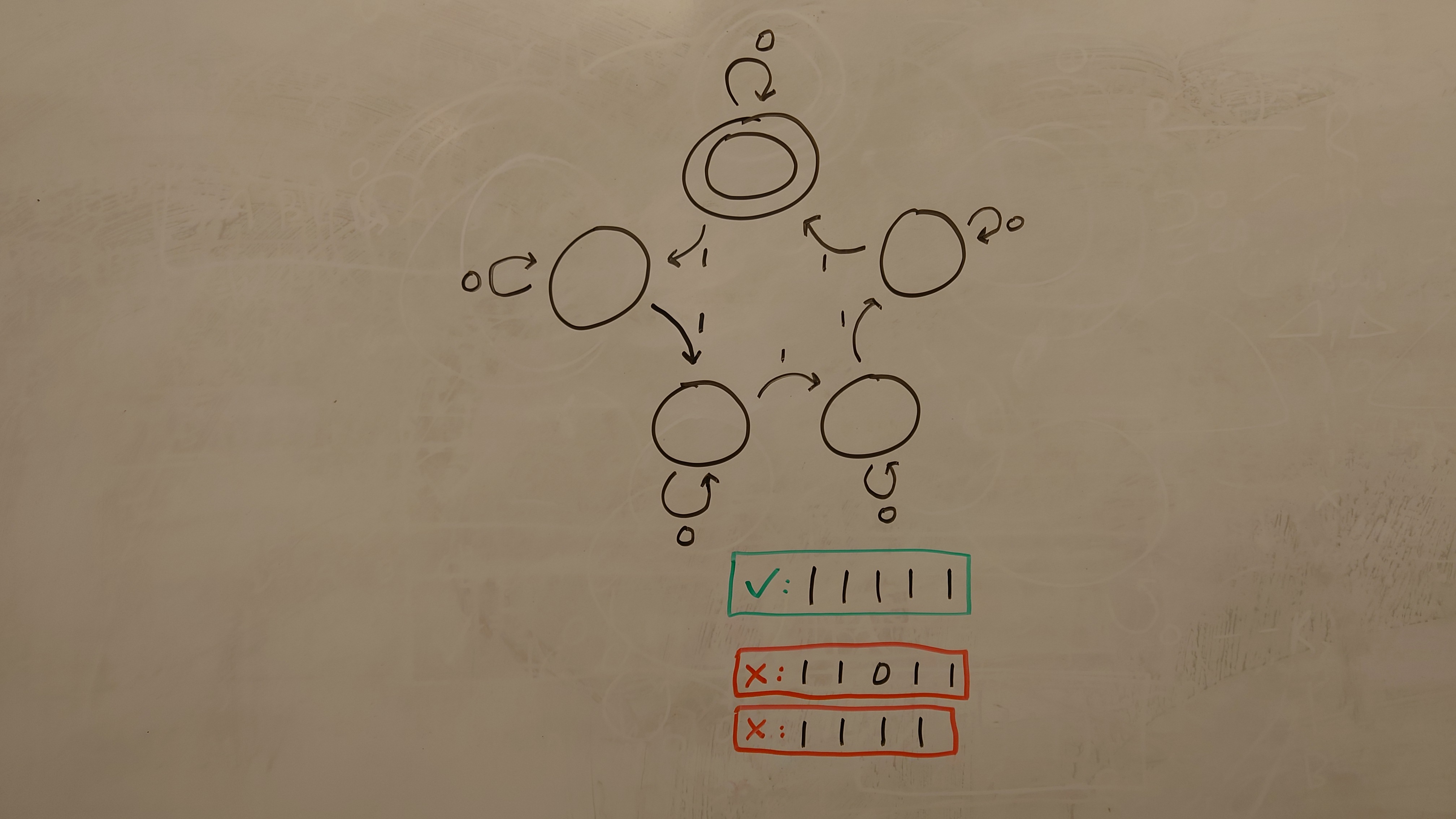Gallery
Click on the automata image to go to its page.
A1
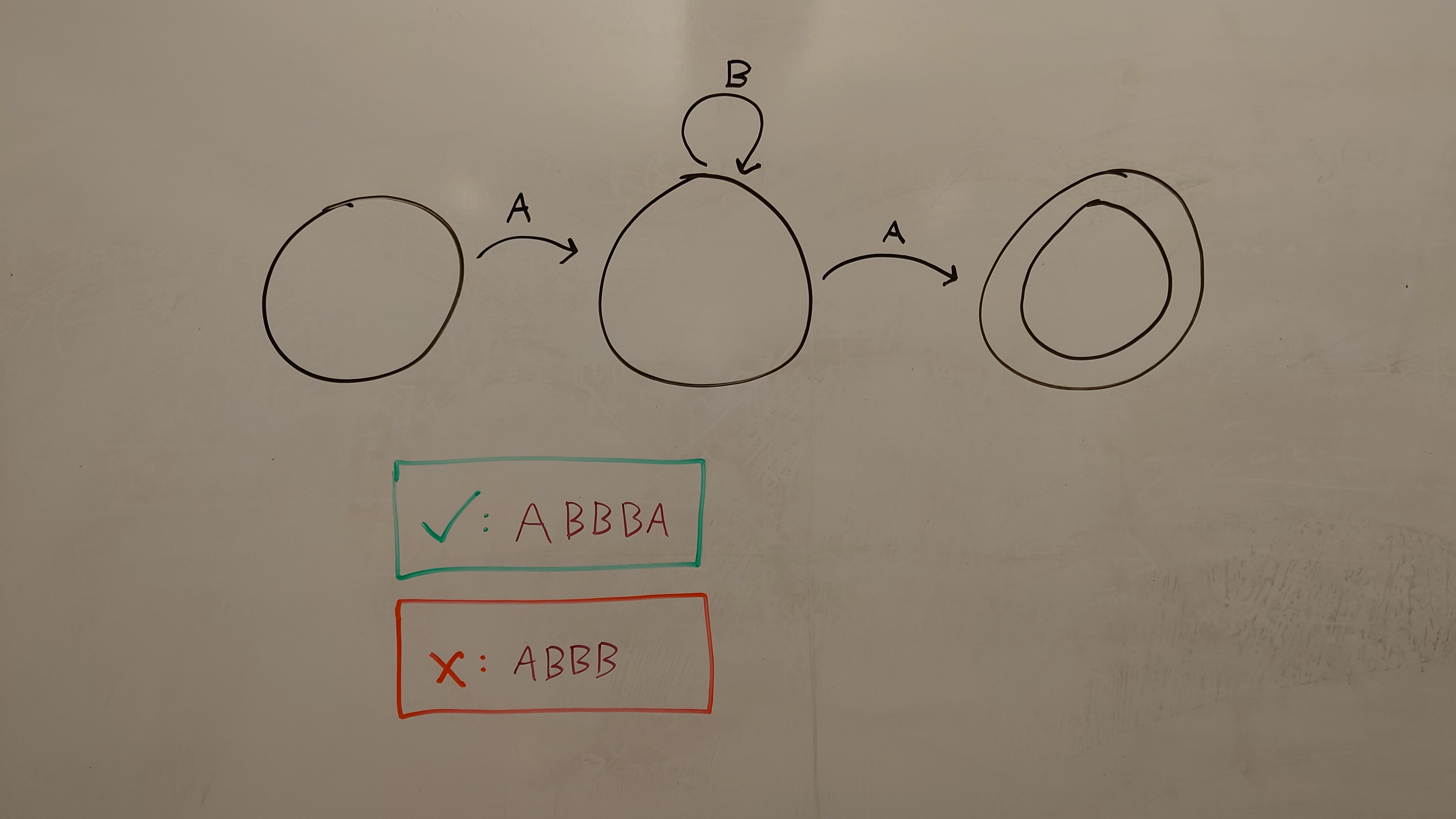
Automaton A1 is the prototypical automaton, drawn as a part of the project proposal. Implementation details were not considered; rather, the implementation evolved to recognize the features present in this image.
A2
Automaton A2 is the simplest automaton, with a single accepting state. Or, it should be, except that it is unrealizable as drawn. The intent of the automaton, as shown in the input examples, is that it accepts all single-character strings `1` and `0`. This requires a second state that transitions to the drawn state on all inputs. This error was not realized until this automaton was synthesized for the first time, illustrating the importance of providing input examples for a sanity check. However, our use of program synthesis lets us simply add an additional "extra" state to the program specification, which generates the intended automaton program.
A3
Automaton A3 is an extension of Automaton A2 (and has the same unrealizability problem). It adds a longer example input box, as well as transitions that go in both directions between two states.
Odd One
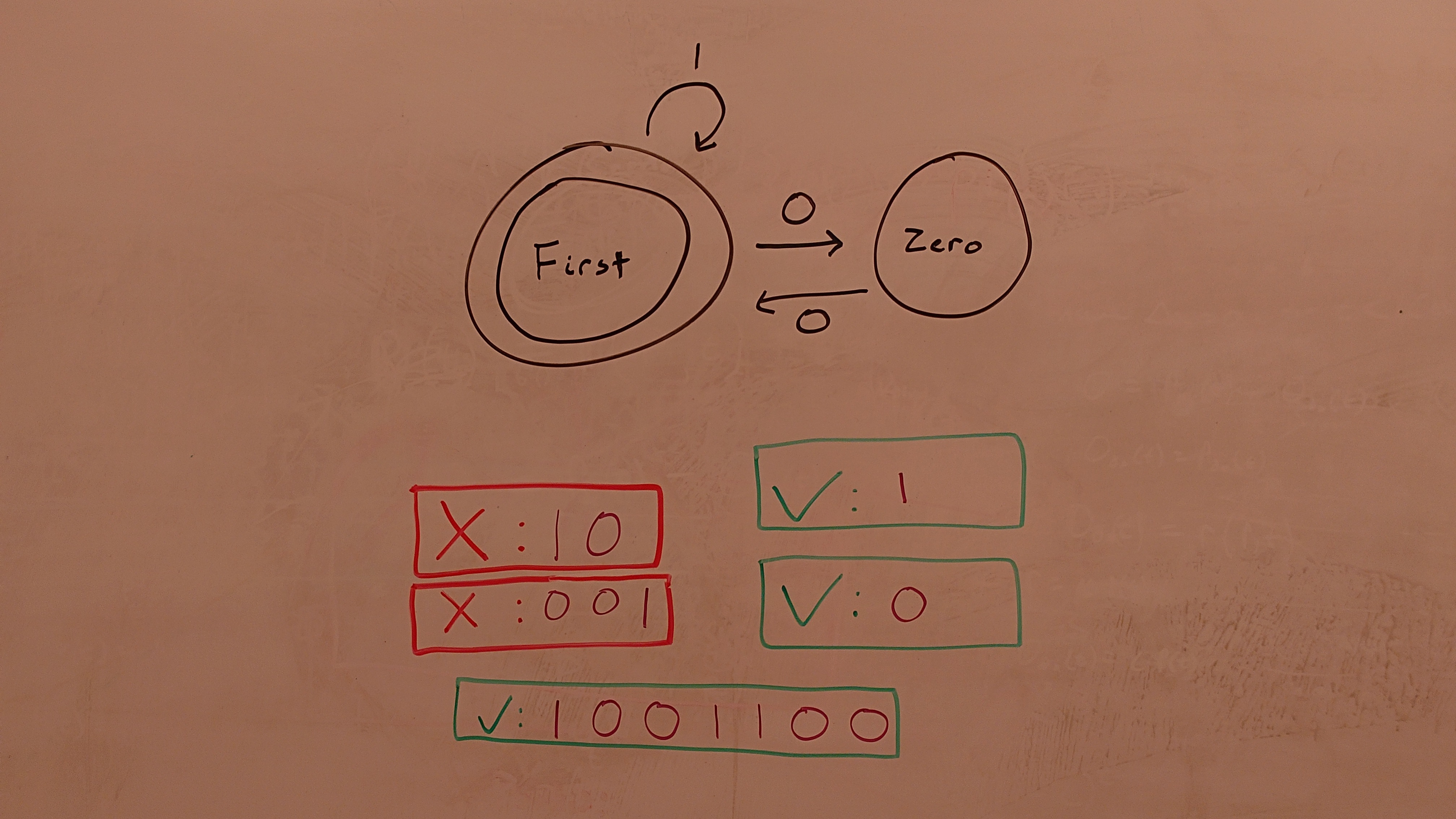
Odd One accepts all strings starting and ending with some number of zeros, including an odd number of contiguous ones between the zeros.
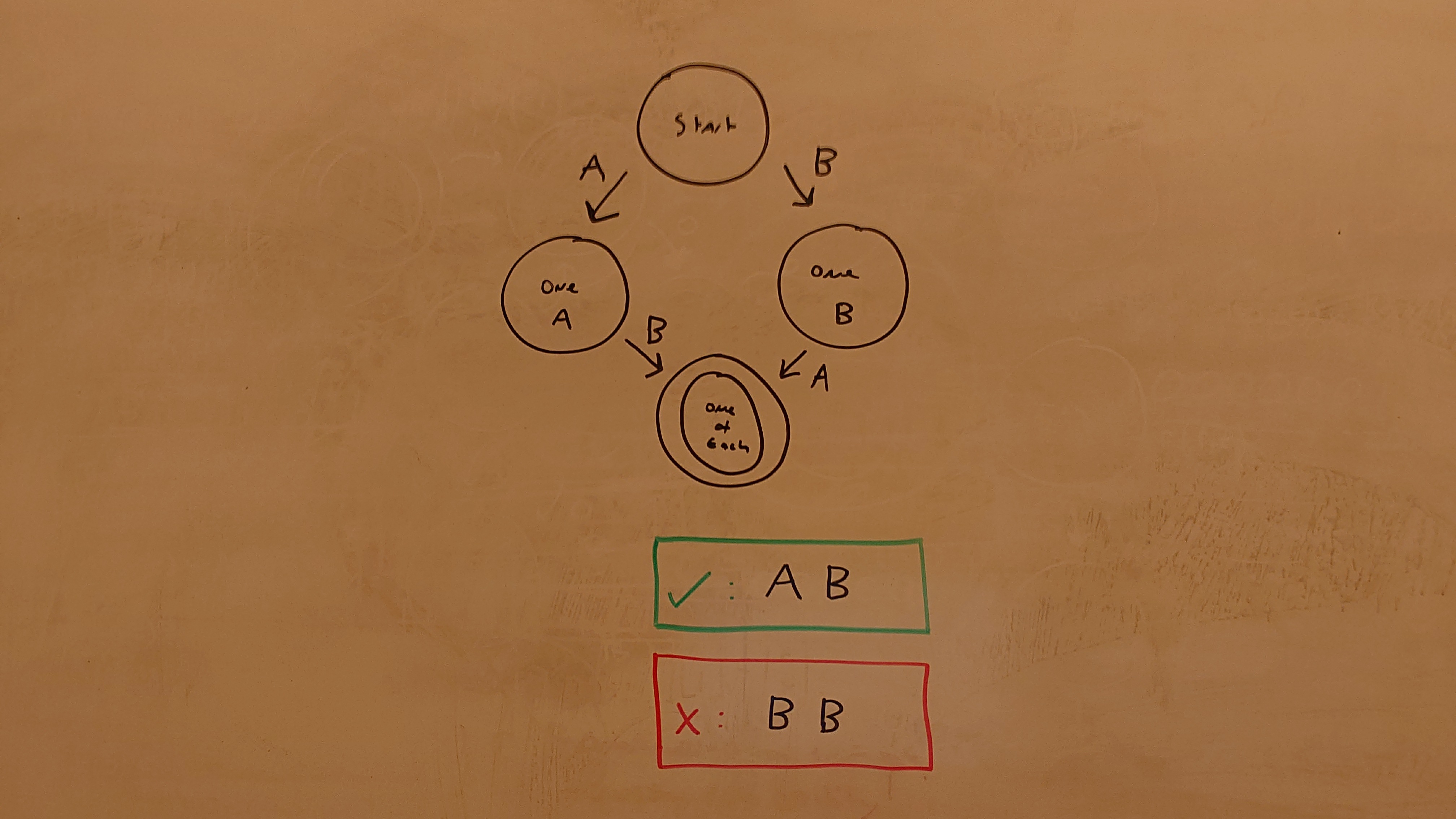
One of Each
More details about One of Each
One of Each only accepts strings that have one A and one B; that is, only AB and BA. Note how the top of this image is slightly defocused, which the feature extraction is robust to.
Stutter
Stutter accepts strings where each character appears in a pair with itself; every character must be doubled.
Multiple of Three
More details about Multiple of Three
Multiple of Three accepts all binary strings that are a multiple of three. This automaton was transcribed from the Wikipedia page on deterministic finite automaton. The "whiteboard noise" is getting strong; pieces of previous automata are beginning to become clearly visible in the background.
ASCII Digits
More details about ASCII Digits
ASCII Digits accepts all binary strings that represent digits zero through 9 in ASCII. This automaton is intended to be an extreme case: it contains 12 states (instead of the usual three or four), as well as free text not associated with the automaton itself.
Five Ones
Five Ones accepts all binary strings that have multiples of five ones. Interestingly, this is the same automaton as drawn as a \(5n+k\) automaton: only the initial state differentiates between these. Here, the given examples disambiguate this case. One positive example is sufficient; however, four negative examples would be required without any positive example.
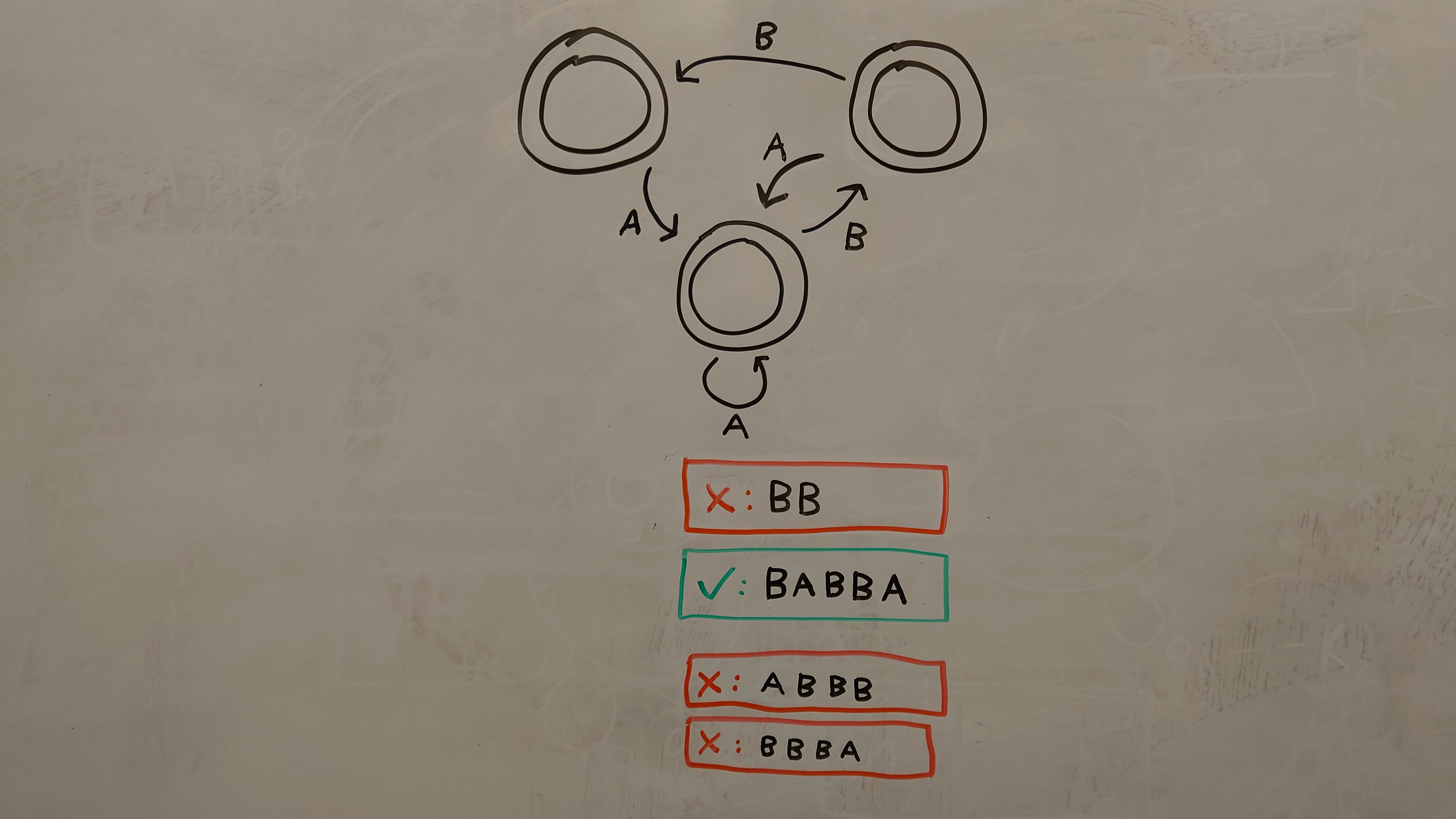
Syllables
Syllables accepts "words" made of "syllables"; that is, no more than two consonants (B) without a vowel (A). The design of this automaton illustrates the value of providing examples: the bottom state was initally intended to be the initial state; however, after providing "BB" as a negative example, the initial state needs to be the right-most state to satisfy the actual intent.