optim::optpp::StaticOptppOptimizer< Method, Objective, Constraint > Class Template Reference

This is the core class for running optimization. More...

List of all members.

Public Member Functions
void	Destruct ()
void	Destruct ()
void	Init (fx_module *module, Objective *objective)
void	Init (fx_module *module, Objective *objective)
void	Optimize (Vector *result)
void	Optimize (Vector *result)

---

Detailed Description

template<typename Method, typename Objective, ConstraintType Constraint>
class optim::optpp::StaticOptppOptimizer< Method, Objective, Constraint >

This is the core class for running optimization.

It supports everything that opt++ offers, constrained and unconstrained optimization, linear/nonlinear equalities/ineqialities as well as bound constraints. The algorithms include zero order methods (derivative free) up to second order (Newton's method).

template <typename Method, typename Objective, ConstraintType Constraint> class StaticOptppOptimizer;

Parameters:

	Method	the optimization method we are going to use, it can be any of the following: typedef OPTPP::OptCG CG; // for conjugate gradient typedef OPTPP::OptQNewton QNewton; // for quasi newton method typedef OPTPP::OptQNewton BFGS; // for BFGS typedef OPTPP::OptFDNewton FDNewton;// for newton with finite differences typedef OPTPP::OptNewton Newton; // for standard newton typedef OPTPP::OptLBFGS LBFGS; // for limited BFGS
	Constraint	It can be any sum of the following enums enum ConstraintType { NoConstraint = 0, // unconstrained optimization BoundConstraint = 2, // box constraints LinearEquality = 4, // linear equalities LinearInequality = 8, // linear inequalities NonLinearEquality = 16, // nonlinear equalities NonLinearInequality= 32 // nonlinear inequalities };
	Objective	This is the class that defines the objective ant the constraints, as well as initializations. You can use any class that defines the following member functions:

Note:

Not every function has to be defined. For example if you are using a first order method that requires gradient only, you don't need to define ComputeHessian. Another example, if you are using only linear equality constraints you don't need to define the functions that have to do with nonlinear equality or inequality constraints.

    class MyOptimizationProblem {
      public:
       // returns the dimensionality of the optimization
       //   also known as the number of the optimization variable
       index_t dimension(); 
       
       // fills the vector with initial value
       void GiveInit(Vector *vec); 
       
       // Computes the objective f(x) and returns it to value
       void ComputeObjective(Vector &x, double *value);
       
       // Computes the gradient g=f'(x)
       void ComputeGradient(Vector &x, Vector *g);
       
       // Computes the Hessian  h=f''(x);
       void ComputeHessian(Vector &x, Matrix *h);
     
       // Defines the Bound constraints for the variables
       void GetBoundConstraint(Vector *lower_bound, Vector *upper_bound);

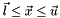The Vectors lower_bound and upper_bound contain the lower and upper bounds for all the constraints. If you want to have only lower bounds then leave the upper_bound vector unchanged. If you want only upper bounds then leave the lower bound unchanged.

       // Fills the matrix A and vector b for equality constraints 
       void GetLinearEquality(Matrix *a_mat, Vector *b_vec);

The constraint is expressed in the form

       // Fills the matrix A, lower and upper bounds for the linear
       // inequalities
       void GetLinearInequality(Matrix *a_mat, Vector *l_vec, Vector *u_vec);

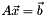
The constraint is expressed in the form 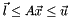if you have only left or right hand side inequality, just do nothing about the one you don't care.

       // Returns the number of nonlinear equalities
       index_t num_of_non_linear_equalities()    

       // Writes on vecc the evaluation of nonlinear equality constraints on
       // vecx
       void ComputeNonLinearEqualityConstraints(Vector &vecx, Vector *vecc);
       
       // Writes on cjacob  the evaluation of the jacobian nonlinear equality 
       // constraints on vecx
       void ComputeNonLinearEqualityConstraintsJacobian(Vector &vecx, Matrix *cjacob);
       
       // Returns the number of nonlinear inequalities
       index_t num_of_non_linear_inequalities()    
       
       // Writes on vecc the evaluation of nonlinear inequality constraints on
       // vecx
       void ComputeNonLinearInequalityConstraints(Vector &vecx, Vector *vecc);
       
       // Writes on cjacob  the evaluation of the jacobian nonlinear equality 
       // constraints on vecx
       void ComputeNonLinearInequalityConstraintsJacobian(Vector &vecx, Matirx *cjacob);
       
       // Writes on both vectors the lower and upper bounds of nonlinear
       // inequalities 
       void GetNonLinearInequalityConstraintBounds(Vector *lower, Vector *upper);

The constraint is expressed in the form 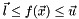, if you want only one side inequality then ignore the side you are not interested in. If you don't specify any of 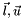then it assumes the inequality .

    };

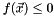Definition at line 651 of file optimizer.h.

---

The documentation for this class was generated from the following files:

• fastlib/optimization/optpp/optimizer.h
• include/fastlib/optimization/optpp/optimizer.h