la Namespace Reference

Linear-algebra routines. More...

Functions
void	AddExpert (double alpha, const Matrix &X, Matrix *Y)
	Adds a scaled matrix to an existing matrix (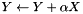 $Y \gets Y + \alpha X$ ).
void	AddExpert (double alpha, const Vector &x, Vector *y)
	Adds a scaled vector to an existing vector (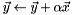 $\vec{y} \gets \vec{y} + \alpha \vec{x}$ ).
void	AddExpert (index_t length, double alpha, const double x, double y)
void	AddInit (const Matrix &X, const Matrix &Y, Matrix *Z)
	Inits a matrix to the sum of two matrices (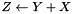 $Z \gets Y + X$ ).
void	AddInit (const Vector &x, const Vector &y, Vector *z)
	Inits a vector to the sum of two vectors (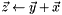 $\vec{z} \gets \vec{y} + \vec{x}$ ).
void	AddOverwrite (const Matrix &X, const Matrix &Y, Matrix *Z)
	Sets a matrix to the sum of two matrices (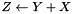 $Z \gets Y + X$ ).
void	AddOverwrite (const Vector &x, const Vector &y, Vector *z)
	Sets a vector to the sum of two vectors (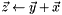 $\vec{z} \gets \vec{y} + \vec{x}$ ).
void	AddOverwrite (index_t length, const double x, const double y, double *z)
void	AddTo (const Matrix &X, Matrix *Y)
	Adds a matrix to an existing matrix (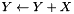 $Y \gets Y + X$ );.
void	AddTo (const Vector &x, Vector *y)
	Adds a vector to an existing vector (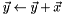 $\vec{y} \gets \vec{y} + \vec{x}$ );.
void	AddTo (index_t length, const double x, double y)
double	DistanceSqEuclidean (const Vector &x, const Vector &y)
	Finds the Euclidean distance squared between two vectors.
double	DistanceSqEuclidean (index_t length, const double va, const double vb)
	Finds the Euclidean distance squared between two vectors.
double	Dot (const Matrix &x, const Matrix &y)
	Finds the dot product of two matrices It is pretty straigth forward, treat matrices as unfolded vectores ( $X \bullet Y$ ).
double	Dot (const Vector &x, const Vector &y)
	Finds the dot product of two vectors (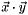 $\vec{x} \cdot \vec{y}$ ).
double	Dot (index_t length, const double x, const double y)
success_t	LeastSquareFit (Matrix &y, Matrix &x, Matrix *a)
	Solves the classic least square problem y=x*a where y is N x r x is N x m a is m x r We require that N >= m a should not be initialized.
success_t	LeastSquareFit (Vector &y, Matrix &x, Vector *a)
	Solves the classic least square problem y=x*a where y is N x 1 x is N x m a is m x 1 We require that N >= m a should not be initialized.
success_t	LeastSquareFitTrans (Matrix &y, Matrix &x, Matrix *a)
	Solves the classic least square problem y=x'*a where y is N x r x is m x N a is m x r We require that N >= m a should not be initialized.
double	LengthEuclidean (const Vector &x)
	Finds the square root of the dot product of a vector with itself (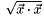 $\sqrt{\vec{x} \cdot \vec{x}}$ ).
double	LengthEuclidean (index_t length, const double *x)
template<int t_pow>
double	LMetric (index_t length, const double va, const double vb)
	Finds an L_p metric distance AND performs the root at the end.
template<int t_pow>
double	RawLMetric (index_t length, const double va, const double vb)
	Finds an L_p metric distance except doesn't perform the root at the end.
void	Scale (double alpha, Matrix *X)
	Scales a matrix in-place by some factor (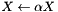 $X \gets \alpha X$ ).
void	Scale (double alpha, Vector *x)
	Scales a vector in-place by some factor (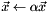 $\vec{x} \gets \alpha \vec{x}$ ).
void	Scale (index_t length, double alpha, double *x)
void	ScaleInit (double alpha, const Matrix &X, Matrix *Y)
	Inits a matrix to another scaled by some factor (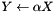 $Y \gets \alpha X$ ).
void	ScaleInit (double alpha, const Vector &x, Vector *y)
	Inits a vector to another scaled by some factor (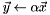 $\vec{y} \gets \alpha \vec{x}$ ).
void	ScaleOverwrite (double alpha, const Matrix &X, Matrix *Y)
	Sets a matrix to another scaled by some factor (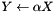 $Y \gets \alpha X$ ).
void	ScaleOverwrite (double alpha, const Vector &x, Vector *y)
	Sets a vector to another scaled by some factor (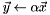 $\vec{y} \gets \alpha \vec{x}$ ).
void	ScaleOverwrite (index_t length, double alpha, const double x, double y)
void	ScaleRows (const Matrix &d, Matrix *X)
	Scales each row of the matrix to a different scale.
void	ScaleRows (const Vector &d, Matrix *X)
	Scales each row of the matrix to a different scale.
void	ScaleRows (index_t n_rows, index_t n_cols, const double scales, double matrix)
	Scales the rows of a column-major matrix by a different value for each row.
void	SubFrom (const Matrix &X, Matrix *Y)
	Subtracts a matrix from an existing matrix (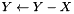 $Y \gets Y - X$ ).
void	SubFrom (const Vector &x, Vector *y)
	Subtracts a vector from an existing vector (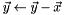 $\vec{y} \gets \vec{y} - \vec{x}$ ).
void	SubFrom (index_t length, const double x, double y)
void	SubInit (const Matrix &X, const Matrix &Y, Matrix *Z)
	Inits a matrix to the difference of two matrices (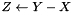 $Z \gets Y - X$ ).
void	SubInit (const Vector &x, const Vector &y, Vector *z)
	Inits a vector to the difference of two vectors (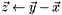 $\vec{z} \gets \vec{y} - \vec{x}$ ).
void	SubOverwrite (const Matrix &X, const Matrix &Y, Matrix *Z)
	Sets a matrix to the difference of two matrices (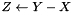 $Z \gets Y - X$ ).
void	SubOverwrite (const Vector &x, const Vector &y, Vector *z)
	Sets a vector to the difference of two vectors (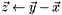 $\vec{z} \gets \vec{y} - \vec{x}$ ).
void	SubOverwrite (index_t length, const double x, const double y, double *z)
double	Trace (Matrix &a)
	Finds the trace of the matrix.
void	TransposeInit (const Matrix &X, Matrix *Y)
	Inits a matrix to the transpose of another (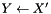 $Y \gets X'$ ).
void	TransposeOverwrite (const Matrix &X, Matrix *Y)
	Sets a matrix to the transpose of another (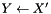 $Y \gets X'$ ).
void	TransposeSquare (Matrix *X)
	Computes a square matrix transpose in-place (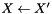 $X \gets X'$ ).

Detailed Description

Linear-algebra routines.

This encompasses most basic real-valued vector and matrix math. Most functions are written in a similar style, so after using a few it should be clear how others are used. For instance, input arguments come first, and the output arguments are last.

Many functions have several versions:

The Init version. This stores the result into a Matrix or Vector which has been declared, but hasn't been initialized. This will call the proper Init function for you. Example:

 void SomeExampleCode(const Matrix& a, const Matrix& b) {
   Matrix c;
   // c must not be initialized
   la::MulInit(a, b, &c);
 }

The Overwrite version. The result is stored in an existing matrix or vector that is the correct size already, overwriting its previous contents, if any. Example:

 void SomeExampleCode(const Matrix& a, const Matrix& b) {
   Matrix c;
   c.Init(a.n_rows(), b.n_cols()); // c must be set to the proper size first
   la::MulOverwrite(a, b, &c);
   // c can be used over again
   la::MulOverwrite(a, b, &c);
 }

The Expert version, or power-user version. We recommend you avoid this version whenever possible. These are the closest mapping to the LAPACK or BLAS routine. These will require that memory for destinations is already allocated but the memory itself is not initalized. These usually take a Matrix or Vector pointer, or sometimes just a pointer to a slab of doubles. Sometimes, one of the "inputs" is completely destroyed while LAPACK performs its computations.

FINAL WARNING: With all of these routines, be very careful about passing in an argument as both a source and destination -- usually this is an error and will result in garbage results, except for simple addition/scaling/subtraction.

Function Documentation

void la::AddExpert	(	double	alpha,
		const Matrix &	X,
		Matrix *	Y
	)			`[inline]`

Adds a scaled matrix to an existing matrix (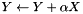 $Y \gets Y + \alpha X$ ).

Definition at line 418 of file uselapack.h.

void la::AddExpert	(	double	alpha,
		const Vector &	x,
		Vector *	y
	)			`[inline]`

Adds a scaled vector to an existing vector (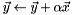 $\vec{y} \gets \vec{y} + \alpha \vec{x}$ ).

Definition at line 410 of file uselapack.h.

References GenVector< T >::length(), and GenVector< T >::ptr().

void la::AddInit	(	const Matrix &	X,
		const Matrix &	Y,
		Matrix *	Z
	)			`[inline]`

Inits a matrix to the sum of two matrices (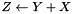 $Z \gets Y + X$ ).

Definition at line 477 of file uselapack.h.

void la::AddInit	(	const Vector &	x,
		const Vector &	y,
		Vector *	z
	)			`[inline]`

Inits a vector to the sum of two vectors (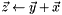 $\vec{z} \gets \vec{y} + \vec{x}$ ).

Definition at line 469 of file uselapack.h.

References GenVector< T >::Init(), and GenVector< T >::length().

void la::AddOverwrite	(	const Matrix &	X,
		const Matrix &	Y,
		Matrix *	Z
	)			`[inline]`

Sets a matrix to the sum of two matrices (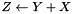 $Z \gets Y + X$ ).

Definition at line 457 of file uselapack.h.

void la::AddOverwrite	(	const Vector &	x,
		const Vector &	y,
		Vector *	z
	)			`[inline]`

Sets a vector to the sum of two vectors (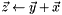 $\vec{z} \gets \vec{y} + \vec{x}$ ).

Definition at line 448 of file uselapack.h.

References GenVector< T >::length(), and GenVector< T >::ptr().

void la::AddTo	(	const Matrix &	X,
		Matrix *	Y
	)			`[inline]`

Adds a matrix to an existing matrix (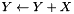 $Y \gets Y + X$ );.

Definition at line 438 of file uselapack.h.

void la::AddTo	(	const Vector &	x,
		Vector *	y
	)			`[inline]`

Adds a vector to an existing vector (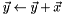 $\vec{y} \gets \vec{y} + \vec{x}$ );.

Definition at line 430 of file uselapack.h.

References GenVector< T >::length(), and GenVector< T >::ptr().

double la::DistanceSqEuclidean	(	const Vector &	x,
		const Vector &	y
	)			`[inline]`

Finds the Euclidean distance squared between two vectors.

Definition at line 68 of file la.h.

References DistanceSqEuclidean(), GenVector< T >::length(), and GenVector< T >::ptr().

double la::DistanceSqEuclidean	(	index_t	length,
		const double *	va,
		const double *	vb
	)			`[inline]`

Finds the Euclidean distance squared between two vectors.

Definition at line 56 of file la.h.

Referenced by NaiveKde< TKernel >::Compute(), AllkNN::ComputeBaseCase_(), AllkFN::ComputeBaseCase_(), DistanceSqEuclidean(), DiskAllNN::GNPBaseCase_(), and AllNN::GNPBaseCase_().

double la::Dot	(	const Matrix &	x,
		const Matrix &	y
	)			`[inline]`

Finds the dot product of two matrices It is pretty straigth forward, treat matrices as unfolded vectores ( $X \bullet Y$ ).

Definition at line 322 of file uselapack.h.

double la::Dot	(	const Vector &	x,
		const Vector &	y
	)			`[inline]`

Finds the dot product of two vectors (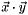 $\vec{x} \cdot \vec{y}$ ).

Definition at line 312 of file uselapack.h.

References GenVector< T >::length(), and GenVector< T >::ptr().

success_t la::LeastSquareFit	(	Matrix &	y,
		Matrix &	x,
		Matrix *	a
	)			`[inline]`

Solves the classic least square problem y=x*a where y is N x r x is N x m a is m x r We require that N >= m a should not be initialized.

Definition at line 150 of file la.h.

References linalg__private::MulTransAInit().

success_t la::LeastSquareFit	(	Vector &	y,
		Matrix &	x,
		Vector *	a
	)			`[inline]`

Solves the classic least square problem y=x*a where y is N x 1 x is N x m a is m x 1 We require that N >= m a should not be initialized.

Definition at line 125 of file la.h.

References GenVector< T >::length(), linalg__private::MulInit(), and linalg__private::MulTransAInit().

success_t la::LeastSquareFitTrans	(	Matrix &	y,
		Matrix &	x,
		Matrix *	a
	)			`[inline]`

Solves the classic least square problem y=x'*a where y is N x r x is m x N a is m x r We require that N >= m a should not be initialized.

Definition at line 175 of file la.h.

References linalg__private::MulInit(), and linalg__private::MulTransBInit().

double la::LengthEuclidean ( const Vector & x ) [inline]

Finds the square root of the dot product of a vector with itself (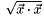 $\sqrt{\vec{x} \cdot \vec{x}}$ ).

Definition at line 304 of file uselapack.h.

References GenVector< T >::length(), and GenVector< T >::ptr().

template<int t_pow>

double la::LMetric	(	index_t	length,
		const double *	va,
		const double *	vb
	)			`[inline]`

Finds an L_p metric distance AND performs the root at the end.

Parameters:

	t_pow	the power each distance calculatin is raised to
	length	the length of the vectors
	va	first vector
	vb	second vector

Definition at line 101 of file la.h.

template<int t_pow>

double la::RawLMetric	(	index_t	length,
		const double *	va,
		const double *	vb
	)			`[inline]`

Finds an L_p metric distance except doesn't perform the root at the end.

Parameters:

	t_pow	the power each distance calculatin is raised to
	length	the length of the vectors
	va	first vector
	vb	second vector

Definition at line 82 of file la.h.

void la::Scale	(	double	alpha,
		Matrix *	X
	)			`[inline]`

Scales a matrix in-place by some factor (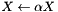 $X \gets \alpha X$ ).

Definition at line 341 of file uselapack.h.

void la::Scale	(	double	alpha,
		Vector *	x
	)			`[inline]`

Scales a vector in-place by some factor (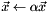 $\vec{x} \gets \alpha \vec{x}$ ).

Definition at line 334 of file uselapack.h.

References GenVector< T >::length(), and GenVector< T >::ptr().

void la::ScaleInit	(	double	alpha,
		const Matrix &	X,
		Matrix *	Y
	)			`[inline]`

Inits a matrix to another scaled by some factor (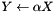 $Y \gets \alpha X$ ).

Definition at line 399 of file uselapack.h.

void la::ScaleInit	(	double	alpha,
		const Vector &	x,
		Vector *	y
	)			`[inline]`

Inits a vector to another scaled by some factor (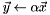 $\vec{y} \gets \alpha \vec{x}$ ).

Definition at line 391 of file uselapack.h.

References GenVector< T >::Init(), and GenVector< T >::length().

Referenced by KalmanFiltTimeInvariantMstUpdate().

void la::ScaleOverwrite	(	double	alpha,
		const Matrix &	X,
		Matrix *	Y
	)			`[inline]`

Sets a matrix to another scaled by some factor (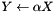 $Y \gets \alpha X$ ).

Definition at line 381 of file uselapack.h.

void la::ScaleOverwrite	(	double	alpha,
		const Vector &	x,
		Vector *	y
	)			`[inline]`

Sets a vector to another scaled by some factor (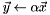 $\vec{y} \gets \alpha \vec{x}$ ).

Definition at line 373 of file uselapack.h.

References GenVector< T >::length(), and GenVector< T >::ptr().

void la::ScaleRows	(	const Matrix &	d,
		Matrix *	X
	)			`[inline]`

Scales each row of the matrix to a different scale.

X <- diag(d) * X

Parameters:

	d	is an one dimensional matrix (1xM or Mx1);
	X	the matrix to scale

Definition at line 364 of file uselapack.h.

References ScaleRows().

void la::ScaleRows	(	const Vector &	d,
		Matrix *	X
	)			`[inline]`

Scales each row of the matrix to a different scale.

X <- diag(d) * X

Parameters:

	d	a length-M vector with each value corresponding
	X	the matrix to scale

Definition at line 352 of file uselapack.h.

References GenVector< T >::length(), GenVector< T >::ptr(), and ScaleRows().

void la::ScaleRows	(	index_t	n_rows,
		index_t	n_cols,
		const double *	scales,
		double *	matrix
	)			`[inline]`

Scales the rows of a column-major matrix by a different value for each row.

Definition at line 136 of file uselapack.h.

Referenced by DoSvmNormalize(), and ScaleRows().

void la::SubFrom	(	const Matrix &	X,
		Matrix *	Y
	)			`[inline]`

Subtracts a matrix from an existing matrix (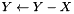 $Y \gets Y - X$ ).

Definition at line 496 of file uselapack.h.

void la::SubFrom	(	const Vector &	x,
		Vector *	y
	)			`[inline]`

Subtracts a vector from an existing vector (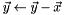 $\vec{y} \gets \vec{y} - \vec{x}$ ).

Definition at line 488 of file uselapack.h.

References GenVector< T >::length(), and GenVector< T >::ptr().

void la::SubInit	(	const Matrix &	X,
		const Matrix &	Y,
		Matrix *	Z
	)			`[inline]`

Inits a matrix to the difference of two matrices (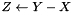 $Z \gets Y - X$ ).

Definition at line 535 of file uselapack.h.

void la::SubInit	(	const Vector &	x,
		const Vector &	y,
		Vector *	z
	)			`[inline]`

Inits a vector to the difference of two vectors (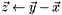 $\vec{z} \gets \vec{y} - \vec{x}$ ).

Definition at line 527 of file uselapack.h.

References GenVector< T >::Init(), and GenVector< T >::length().

void la::SubOverwrite	(	const Matrix &	X,
		const Matrix &	Y,
		Matrix *	Z
	)			`[inline]`

Sets a matrix to the difference of two matrices (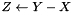 $Z \gets Y - X$ ).

Definition at line 515 of file uselapack.h.

void la::SubOverwrite	(	const Vector &	x,
		const Vector &	y,
		Vector *	z
	)			`[inline]`

Sets a vector to the difference of two vectors (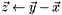 $\vec{z} \gets \vec{y} - \vec{x}$ ).

Definition at line 506 of file uselapack.h.

References GenVector< T >::length(), and GenVector< T >::ptr().

double la::Trace ( Matrix & a ) [inline]

Finds the trace of the matrix.

Trace(A) is the sum of the diagonal elements

Definition at line 108 of file la.h.

void la::TransposeInit	(	const Matrix &	X,
		Matrix *	Y
	)			`[inline]`

Inits a matrix to the transpose of another (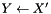 $Y \gets X'$ ).

Definition at line 582 of file uselapack.h.

References TransposeOverwrite().

Referenced by DoSvmNormalize(), MoGL2E::InitialPointGenerator(), KalmanFiltTimeInvariantMstUpdate(), KalmanFiltTimeInvariantTimeUpdate(), RandVector(), and linalg__private::SaveCorrectly().

void la::TransposeOverwrite	(	const Matrix &	X,
		Matrix *	Y
	)			`[inline]`

Sets a matrix to the transpose of another (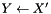 $Y \gets X'$ ).

Definition at line 567 of file uselapack.h.

Referenced by MoGL2E::MakeModel(), MoGL2E::MakeModelWithGradients(), and TransposeInit().

void la::TransposeSquare ( Matrix * X ) [inline]

Computes a square matrix transpose in-place (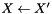 $X \gets X'$ ).

Definition at line 551 of file uselapack.h.

la Namespace Reference

Functions

Detailed Description

Function Documentation