For count BOWs, the feasible set
![]() is the set of permutations on
words in
is the set of permutations on
words in
![]() . This set will be large for indices of even
moderate size, so it is impractical to enumerate documents
. This set will be large for indices of even
moderate size, so it is impractical to enumerate documents
![]() . Instead, we approximately find the best document using memory-bounded
A
. Instead, we approximately find the best document using memory-bounded
A![]() search [Russell and Norvig2002]. A
search [Russell and Norvig2002]. A![]() search finds the minimal-cost
path between a start and goal in a search space. It requires a measure
search finds the minimal-cost
path between a start and goal in a search space. It requires a measure ![]() of
the cost from the start state to a particular state, and a heuristic estimate
of
the cost from the start state to a particular state, and a heuristic estimate
![]() of the cost from the state to the goal state. If the estimate
of the cost from the state to the goal state. If the estimate ![]() always
underestimates the true cost to the goal,
always
underestimates the true cost to the goal, ![]() is called an admissible heuristic,
and A
is called an admissible heuristic,
and A![]() search is guaranteed to find the minimal-cost path from start to
goal.
search is guaranteed to find the minimal-cost path from start to
goal.
To find
![]() using A
using A![]() search, let each state in the search space
represent a partial path
search, let each state in the search space
represent a partial path ![]() , where
, where ![]() is the length of the partial path.
The start state consists of the start-of-sentence symbol
is the length of the partial path.
The start state consists of the start-of-sentence symbol
![]() . The ``real''
goal state is the original document, but since this original document is
unknown, the first complete path of length
. The ``real''
goal state is the original document, but since this original document is
unknown, the first complete path of length ![]() that is found is accepted as the
goal. In the absence of search error, this will be the most likely length-
that is found is accepted as the
goal. In the absence of search error, this will be the most likely length-![]() path.
path.
For our ![]() and
and ![]() , it is convenient to use score instead of
cost; A
, it is convenient to use score instead of
cost; A![]() search then maximizes path score instead minimizing path
cost. The partial path score
search then maximizes path score instead minimizing path
cost. The partial path score ![]() of a partial document is the log probability
of the partial document under a language model:
of a partial document is the log probability
of the partial document under a language model:
![]() .
We use the Google Web 1T 5-gram corpus and a 5-gram language model with stupid
backoff [Brants
.
We use the Google Web 1T 5-gram corpus and a 5-gram language model with stupid
backoff [Brants

2007] to approximate the probabilities:
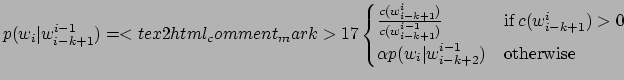 |
We present two heuristics for ![]() below: one that is admissible (i.e., always
overestimates the score of the future path from the current state to the goal),
and one that is not admissible but empirically performs better.
below: one that is admissible (i.e., always
overestimates the score of the future path from the current state to the goal),
and one that is not admissible but empirically performs better.