An admissible heuristic

We exploit properties of the stupid-backoff language model to construct an efficient admissible heuristic. Let $s(w_i\vert w_{i-k+1}^{i-1})=$

$$\max{}_{j=1}^k \alpha^{k-j} \begin{cases} \frac{c(w_{i-j+1}^i)... ... \ c(w_i)/\sum_{v\in \mathrm{vocab}} c(v) & \mathrm{if} j = 1 \end{cases}$$

One can show that $s(w_i\vert w_{i-k+1}^{i-1}) \geq p(w_i\vert w_{i-k+1}^{i-1})$. Let $s^*(w) = \max_{v_1^4 \in \mathrm{vocab}} s(w\vert v_1^4) \geq \max_{v_1^4 \in \mathrm{vocab}} p(w\vert v_1^4)$ be an upper bound on the probability of the word $w \in \mathrm{vocab}$ under all possible 5-gram histories. Then the following is an admissible heuristic:

$$h^{\mathrm{adm}}(w_1^l) = \sum_{w \in \mathbf{x}\backslash w_1^l} \log s^*(w),$$ (1)

where $\mathbf{x}\backslash w_1^l$ denotes the ``remaining BOW'', in which the count $x_v$ is decremented for each occurrence of $v$ in $w_1^l$.

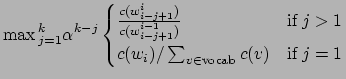The heuristic $h^{\mathrm{adm}}$ can be computed efficiently for each state, since the quantity $s^*$ can be computed once, before A$^*$ search begins. While computing $s^*$, although there are $V^4$ possible permutations $v_1^4 \in \mathrm{vocab}$, we need only consider permutations for which n-gram counts exist; that is, $s^*$ can be computed by scanning the list of n-grams used to construct our language model.