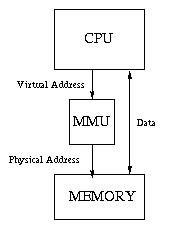
Most modern computers have special hardware called a memory management unit (MMU). This unit sits between the CPU and the memory unit. Whenever the CPU wants to access memory (whether it is to load an instruction or load or store data), it sends the desired memory address to the MMU, which translates it to another address before passing it on the the memory unit. The address generated by the CPU, after any indexing or other addressing-mode arithmetic, is called a virtual address, and the address it gets translated to by the MMU is called a physical address.

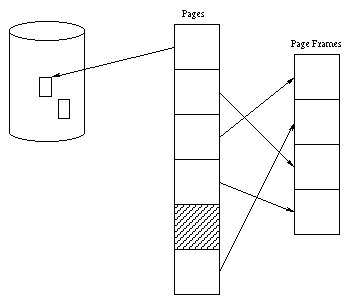
The MMU allows a contiguous region of virtual memory to be mapped to page frames scattered around physical memory making life much easier for the OS when allocating memory. Much more importantly, however, it allows infrequently-used pages to be stored on disk. Here's how it works: The tables used by the MMU have a valid bit for each page in the virtual address space. If this bit is set, the translation of virtual addresses on a page proceeds as normal. If it is clear, any attempt by the CPU to access an address on the page generates an interrupt called a page fault trap. The OS has an interrupt handler for page faults, just as it has a handler for any other kind of interrupt. It is the job of this handler to get the requested page into memory.
In somewhat more detail, when a page fault is generated for page
p1, the interrupt handler does the following:
Page Tables
[Tanenbaum, Section 4.3.2-4]
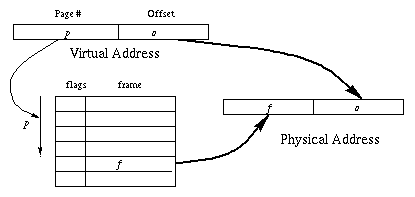
Conceptually, the MMU contains a page table which is simply an
array of entries indexed by page number.
Each entry contains some flags (such as the valid bit mentioned
earlier) and a frame number.
The physical address is formed by concatenating the frame number with the
offset, which is the low-order bits of the virtual address.
Suppose the page size is 4K bytes and a virtual address is 32 bits long (these are typical values for current machines). Then the virtual address would be divided into a 20-bit page number and a 12-bit offset (because 212 = 4096 = 4K), so the page table would have to have 220 = 1,048,576 entries. If each entry is 4 bytes long, that would use up 4 megabytes of memory. And each process has its own page table. Newer machines being introduced now generate 64-bit addresses. Such a machine would need a page table with 4,503,599,627,370,496 entries!
Fortunately, the vast majority of the page table entries are normally marked “invalid.” Although the virtual address may be 32 bits long and thus capable of addressing a virtual address space of 4 gigabytes, a typical process is at most a few megabytes in size, and each megabyte of virtual memory uses only 256 page-table entries (for 4K pages).
There are several different page table organizations use in actual computers. One approach is to put the page table entries in special registers. This was the approach used by the PDP-11 minicomputer introduced in the 1970's. The virtual address was 16 bits and the page size was 8K bytes. Thus the virtual address consisted of 3 bits of page number and 13 bits of offset, for a total of 8 pages per process. The eight page-table entries were stored in special registers. [As an aside, 16-bit virtual addresses means that any one process could access only 64K bytes of memory. Even in those days that was considered too small, so later versions of the PDP-11 used a trick called “split I/D space.” Each memory reference generated by the CPU had an extra bit indicating whether it was an instruction fetch (I) or a data reference (D), thus allowing 64K bytes for the program and 64K bytes for the data.] Putting page table entries in registers helps make the MMU run faster (the registers were much faster than main memory), but this approach has a downside as well. The registers are expensive, so it works for very small page-table size. Also, each time the OS wants to switch processes, it has to reload the registers with the page-table entries of the new process.
A second approach is to put the page table in main memory. The (physical) address of the page table is held in a register. The page field of the virtual address is added to this register to find the page table entry in physical memory. This approach has the advantage that switching processes is easy (all you have to do is change the contents of one register) but it means that every memory reference generated by the CPU requires two trips to memory. It also can use too much memory, as we saw above.
A third approach is to put the page table itself in virtual memory.
The page number extracted from the virtual address is used as a virtual
address to find the page table entry. To prevent an infinite recursion,
this virtual address is looked up using a page table stored in physical memory.
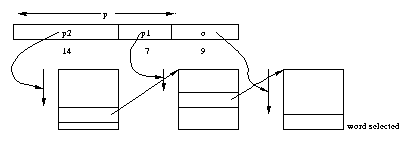
As a concrete example, consider the VAX computer, introduced in the late 70's.
The virtual address of the VAX is 30 bits long, with 512-byte pages (probably
too small even at that time!)
Thus the virtual address a consists of a 21-bit page number
p and a nine-bit offset o.
The page number is multiplied by 4 (the size of a page-table entry) and
added to the contents of the MMU register containing the address of
the page table. This gives a virtual address that is resolved using a
page table in physical memory to get a frame number f1.
In more detail, the high order bits of p index into a table
to find a physical frame number, which, when concatenated with the low bits
of p give the physical address of a word containing f.
The concatenation of f with o is the desired physical
address.
A fourth approach is to use what is called an inverted page table. (Actually, the very first computer to have virtual memory, the Atlas computer built in England in the late 50's used this approach, so in some sense all the page tables described above are “inverted.”) An ordinary page table has an entry for each page, containing the address of the corresponding page frame (if any). An inverted page table has an entry for each page frame, containing the corresponding page number. To resolve a virtual address, the table is searched to find an entry that contains the page number. The good news is that an inverted page table only uses a fixed fraction of memory. For example, if a page is 4K bytes and a page-table entry is 4 bytes, there will be exactly 4 bytes of page table for each 4096 bytes of physical memory. In other words, less that 0.1% of memory will be used for page tables. The bad news is that this is by far the slowest of the methods, since it requires a search of the page table for each reference. The original Atlas machine had special hardware to search the table in parallel, which was reasonable since the table had only 2048 entries.
All of the methods considered thus far can be sped up by using a trick called caching. We will be seeing many many more examples of caching used to speed things up throughout the course. In fact, it has been said that caching is the only technique in computer science used to improve performance. In this case, the specific device is called a translation lookaside buffer (TLB). The TLB contains a set of entries, each of which contains a page number, the corresponding page frame number, and the protection bits. There is special hardware to search the TLB for an entry matching a given page number. If the TLB contains a matching entry, it is found very quickly and nothing more needs to be done. Otherwise we have a TLB miss and have to fall back on one of the other techniques to find the translation. However, we can take that translation we found the hard way and put it into the TLB so that we find it much more quickly the next time. The TLB has a limited size, so to add a new entry, we usually have to throw out an old entry. The usual technique is to throw out the entry that hasn't been used the longest. This strategy, called LRU (least-recently used) replacement is also implemented in hardware. The reason this approach works so well is that most programs spend most of their time accessing a small set of pages over and over again. For example, a program often spends a lot of time in an “inner loop” in one procedure. Even if that procedure, the procedures it calls, and so on are spread over 40K bytes, 10 TLB entries will be sufficient to describe all these pages, and there will no TLB misses provided the TLB has at least 10 entries. This phenomenon is called locality. In practice, the TLB hit rate for instruction references is extremely high. The hit rate for data references is also good, but can vary widely for different programs.
If the TLB performs well enough, it almost doesn't matter how TLB misses are resolved. The IBM Power PC and the HP Spectrum use inverted page tables organized as hash tables in conjunction with a TLB. The MIPS computers (MIPS is now a division of Silicon Graphics) get rid of hardware page tables altogether. A TLB miss causes an interrupt, and it is up to the OS to search the page table and load the appropriate entry into the TLB. The OS typically uses an inverted page table implemented as a software hash table.
Two processes may map the same page number to different page frames. Since the TLB hardware searches for an entry by page number, there would be an ambiguity if entries corresponding to two processes were in the TLB at the same time. There are two ways around this problem. Some systems simply flush the TLB (set a bit in all entries marking them as unused) whenever they switch processes. This is very expensive, not because of the cost of flushing the TLB, but because of all the TLB misses that will happen when the new process starts running. An alternative approach is to add a process identifier to each entry. The hardware then searches on for the concatenation of the page number and the process id of the current process.
We mentioned earlier that each page-table entry contains a “valid” bit as well as some other bits. These other bits include
All of these hardware methods for implementing paging have one thing in common: When the CPU generates a virtual address for which the corresponding page table entry is marked invalid, the MMU generates a page fault interrupt and the OS must handle the fault as explained above. The OS checks its tables to see why it marked the page as invalid. There are (at least) three possible reasons:
We will first consider page-replacement algorithms for a single process,
and then consider algorithms to use when there are multiple processes,
all competing for the same set of frames.
Frame Allocation for a Single Process
Unfortunately, all of these techniques require hardware support and nobody makes hardware that supports them. Thus LRU, in its pure form, is just about as impractical as OPT. Fortunately, it is possible to get a good enough approximation to LRU (which is probably why nobody makes hardware to support true LRU).
There is a curious phenomenon called Belady's Anomaly that comes
up in some algorithms but not others.
Consider the reference string (sequence of page numbers)
0 1 2 3 0 1 4 0 1 2 3 4.
If we use FIFO with three page frames, we get 9 page faults, including
the three faults to bring in the first three pages, but with more memory
(four frames), we actually get more faults (10).
Frame Allocation for Multiple Processes
Up to this point, we have been assuming that there is only one active process. When there are multiple processes, things get more complicated. Algorithms that work well for one process can give terrible results if they are extended to multiple processes in a naive way.
LRU would give excellent results for a single process, and all of the good practical algorithms can be seen as ways of approximating LRU. A straightforward extension of LRU to multiple processes still chooses the page frame that has not been referenced for the longest time. However, that is a lousy idea. Consider a workload consisting of two processes. Process A is copying data from one file to another, while process B is doing a CPU-intensive calculation on a large matrix. Whenever process A blocks for I/O, it stops referencing its pages. After a while process B steals all the page frames away from A. When A finally finishes with an I/O operation, it suffers a series of page faults until it gets back the pages it needs, then computes for a very short time and blocks again on another I/O operation.
There are two problems here. First, we are calculating the time since the last reference to a page incorrectly. The idea behind LRU is “use it or lose it.” If a process hasn't referenced a page for a long time, we take that as evidence that it doesn't want the page any more and re-use the frame for another purpose. But in a multiprogrammed system, there may be two different reasons why a process isn't touching a page: because it is using other pages, or because it is blocked. Clearly, a process should only be penalized for not using a page when it is actually running. To capture this idea, we introduce the notion of virtual time. The virtual time of a process is the amount of CPU time it has used thus far. We can think of each process as having its own clock, which runs only while the process is using the CPU. It is easy for the CPU scheduler to keep track of virtual time. Whenever it starts a burst running on the CPU, it records the current real time. When an interrupt occurs, it calculates the length of the burst that just completed and adds that value to the virtual time of the process that was running. An implementation of LRU should record which process owns each page, and record the virtual time its owner last touched it. Then, when choosing a page to replace, we should consider the difference between the timestamp on a page and the current virtual time of the page's owner. Algorithms that attempt to approximate LRU should do something similar.
There is another problem with our naive multi-process LRU. The CPU-bound process B has an unlimited appetite for pages, whereas the I/O-bound process A only uses a few pages. Even if we calculate LRU using virtual time, process B might occasionally steal pages from A. Giving more pages to B doesn't really help it run any faster, but taking from A a page it really needs has a severe effect on A. A moment's thought shows that an ideal page-replacement algorithm for this particular load would divide into two pools. Process A would get as many pages as it needs and B would get the rest. Each pool would be managed LRU separately. That is, whenever B page faults, it would replace the page in its pool that hadn't been referenced for the longest time.
In general, each process has a set of pages that it is actively using. This set is called the working set of the process. If a process is not allocated enough memory to hold its working set, it will cause an excessive number of page faults. But once a process has enough frames to hold its working set, giving it more memory will have little or no effect.
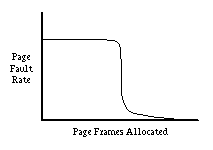
More formally, given a number τ, the working set with parameter τ of a process, denoted Wτ, is the set of pages touched by the process during its most recent τ references to memory. Because most processes have a very high degree of locality, the size of τ is not very important provided it's large enough. A common choice of τ is the number of instructions executed in 1/2 second. In other words, we will consider the working set of a process to be the set of pages it has touched during the previous 1/2 second of virtual time. The Working Set Model of program behavior says that the system will only run efficiently if each process is given enough page frames to hold its working set. What if there aren't enough frames to hold the working sets of all processes? In this case, memory is over-committed and it is hopeless to run all the processes efficiently. It would be better to simply stop one of the processes and give its pages to others.
Another way of looking at this phenomenon is to consider CPU utilization as a function of the level of multiprogramming (number of processes). With too few processes, we can't keep the CPU busy. Thus as we increase the number of processes, we would like to see the CPU utilization steadily improve, eventually getting close to 100%. Realistically, we cannot expect to quite that well, but we would still expect increasing performance when we add more processes.
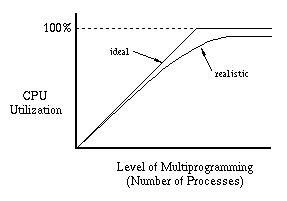
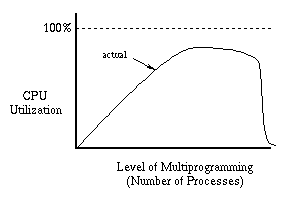
The moral of the story is that there is no point in trying to run more processes than will fit in memory. When we say a process “fits in memory,” we mean that enough page frames have been allocated to it to hold all of its working set. What should we do when we have more processes than will fit? In a batch system (one were users drop off their jobs and expect them to be run some time in the future), we can just delay starting a new job until there is enough memory to hold its working set. In an interactive system, we may not have that option. Users can start processes whenever they want. We still have the option of modifying the scheduler however. If we decide there are too many processes, we can stop one or more processes (tell the scheduler not to run them). The page frames assigned to those processes can then be taken away and given to other processes. It is common to say the stopped processes have been “swapped out” by analogy with a swapping system, since all of the pages of the stopped processes have been moved from main memory to disk. When more memory becomes available (because a process has terminated or because its working set has become smaller) we can “swap in” one of the stopped processes. We could explicitly bring its working set back into memory, but it is sufficient (and usually a better idea) just to make the process runnable. It will quickly bring its working set back into memory simply by causing page faults. This control of the number of active processes is called load control. It is also sometimes called medium-term scheduling as contrasted with long-term scheduling, which is concerned with deciding when to start a new job, and short-term scheduling, which determines how to allocate the CPU resource among the currently active jobs.
It cannot be stressed too strongly that load control is an essential component of any good page-replacement algorithm. When a page fault occurs, we want to make a good decision on which page to replace. But sometimes no decision is good, because there simply are not enough page frames. At that point, we must decide to run some of the processes well rather than run all of them very poorly.
This is a very good model, but it doesn't immediately translate into an algorithm. Various specific algorithms have been proposed. As in the single process case, some are theoretically good but unimplementable, while others are easy to implement but bad. The trick is to find a reasonable compromise.
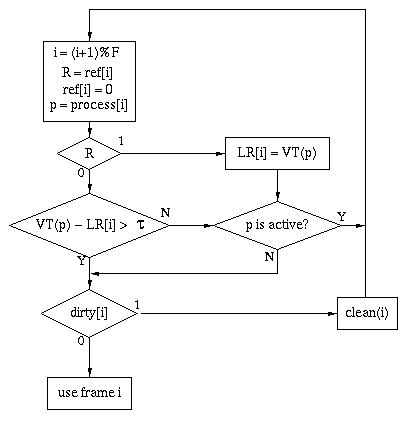
Like CLOCK, WSClock has to be careful to avoid an infinite loop. As in the CLOCK algorithm, it may may a complete circuit of the clock finding only dirty candidate pages. In that case, it has to wait for one of the cleaning requests to finish. It may also find that all pages are unreferenced but "new" (the reference bit is clear but the comparison to tau shows the page has been referenced recently). In either case, memory is overcommitted and some process needs to be stopped.