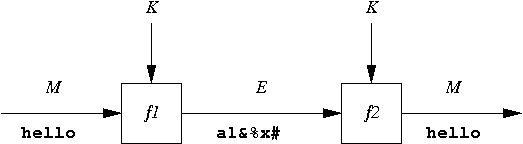
In distributed systems, data is usually sent over insecure channels. A prudent user should assume that it is easy for a "bad guy" to see all the data that goes over the wire. In fact, the bad guy may be assumed to have the power to modify the data as it goes by, delete messages, inject new messages into the stream, or any combination of these operations, such as stealing a message and playing it back at a later time. In such environments, security is based on cryptographic techniques.
Messages are scrambled, or encrypted before they are sent, and decrypted on receipt.
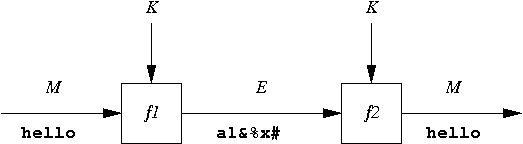
E = f1(M,K)According to the principle of public design, the encryption and decryption functions are well-known publicly available algorithms. It is the key K, known only to the sender and receiver, that provides security.
f2(E,K) = f2(f1(M,K), K) = M
The most important feature of the encryption algorithm f1 is that be infeasible to invert the function. That is, it should be impossible, or at least very hard, to recover M from E without knowing K. In fact, it is quite easy to come up with such an algorithm: exclusive or. If the length of K (in bits) is the same as the length of M, let each bit of E be zero if corresponding bits of M and K are the same, and one if they are different. Another way of looking at this function is that it flips bits of M that correspond to one bits in K and passes through unchanged bits of M in the same position as zero bits of K. In this case, f1 and f2 are the same function. Where there is a zero bit in K the corresponding bit of M passes through both boxes unchanged; where there is a one bit, the input bit gets flipped by the first box and flipped back to its original value by the second box. This algorithm is perfect, from the point of view of invertability. If the bits of K are all chosen at random, knowing E tells you absolutely nothing about M.
However, it has one fatal flaw: The key has to be the same length as the message, and you can only use it once (in the jargon of encryption, this is a one-time pad cipher). Encryption algorithms have been devised with fixed-length keys of 100 or so bits (regardless of the length of M) with the property that M is provably hard (computationally infeasible) to recover from E even if the bad guy
Even with such an algorithm in hand, there's still the problem of how the two parties who wish to communicate get the same key in the first place -- the key distribution problem. If the key is sent over the network without encryption, a bad guy could see it and it would become useless. But if the key is to be sent encrypted, the two sides have to somehow agree on a key to encrypt the key, which leaves us back where we started. One could always send the key through some other means, such as a trusted courier (think of James Bond with a briefcase handcuffed to his wrist). This is called "out-of-band" transmission. It tends to be expensive and introduces risks of its own (see any James Bond movie for examples). Ultimately, some sort of out-of-band transmission is required to get things going, but we would like to minimize it.
A clever partial solution to the key distribution problem was devised by Needham and Schroeder. The algorithm is a bit complicated, and would be totally unreadable without some helpful abbreviations. Instead denoting the result of encrypting message M with key K with the expression f1(M,K), we will write it as [M]K. Think of this as a box with M inside secured with a lock that can only be opened with key K. We will assume that there is a trusted Key Distribution Center (KDC) that helps processes exchange keys with each other securely. A the beginning of time, each process A has a key KA that is known only to A and the KDC. Perhaps these keys were distributed by some out-of-band technique. For example, the software for process A may have been installed from a (trusted!) floppy disk that also contained a key for A to use. The algorithm uses five messages.
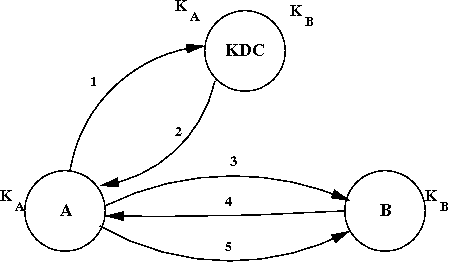
1: request + id(In these examples, "+" represents concatenation of messages.)
The KDC makes up a brand new key Kc which it sends back to A in a rather complicated message.
2: [Kc + id + request + [Kc + A]KB]KAFirst note that the entire message is encrypted with A's key KA. The encryption serves two purposes. First, it prevents any eavesdropper from opening the message and getting at the contents. Only A can open it. Second, it acts as a sort of signature. When A successfully decrypts the message, it knows it must have come from the KDC and not an imposter, since only the KDC (besides A itself) knows KA and could use it to create a message that properly decrypts.1
A saves the key Kc from the body of the message for later use in communicating with B. The original request is included in the response so that A can see that nobody modified the request on its way to KDC. The inclusion of id proves that this is a response to the request just sent, not an earlier response intercepted by the bad guy and retransmitted now. The last component of the response is itself encrypted with B's key. A does not know B's key, so it cannot decrypt this component, but it doesn't have to. It just sends it to B as message 3.
3: [Kc + A]KBAs with message 2, the encryption by KB serves both to hide Kc from eavesdroppers and to certify to B that the message is legitimate. Since only the KDC and B know KB, when B successfully decrypts this message, it knows that the message was prepared by the KDC. A and B now know the new key Kc, and can use it to communicate securely. However, there are two more messages in the protocol.
Messages 4 and 5 are used by B to verify that the message 3 was not a replay. B chooses another random number id' and sends it to A encrypted with the new key Kc. A decrypts the message, modifies the random number in some well-defined way (for example, it adds one to it), re-encrypts it and sends it back.
4: [ id' ]KcThis is an example of a challenge/response protocol.
5: [ f(id') ] Kc
In the 1970's, Diffie and Hellman invented a revolutionary new way of doing encryption, called public-key (or asymmetric) cryptography. At first glance, the change appears minor. Instead of using the same key to encrypt and decrypt, this method uses two different keys, one for encryption and one for decryption. Diffie and Hellman invented an algorithm for generating a pair of keys (P,S) and an encryption algorithm such that messages encrypted with key P can be decrypted only with key S.
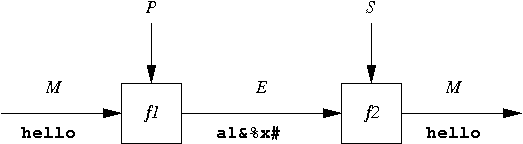
f(f(M,P), S) = f(f(M,S), P) = M.
The beauty of public key cryptography is that if I want you to send me a secret message, all I have to do is generate a key pair (P,S) and send you the key P. You encrypt the message with P and I decrypt it with S. I don't have to worry about sending P across the network without encrypting it. If a bad guy intercepts it, there's nothing he can do with it that can harm me (there's no way to compute S from P or vice versa). S is called the secret key and the P is the public key.
However, there's a catch. A bad guy could pretend to be me and send you his own public key Pbg, claiming it was my public key. If you encrypt the message using Pbg, the bad guy could intercept it and decrypt it, since he knows the corresponding Sbg. Thus my problem is not how to send my public key to you securely, it is how to convince you that it really is mine. We'll see in a minute a (partial) solution to this problem.
Public key encryption is particularly handy for digital signatures. Suppose I want to send you a message M in such a way as to assure you it really came from me. First I compute a hash function h(M) from M using a cryptographic hash function f. Then I encrypt h(M) using my secret key S. I send you both M and the signature [h(M)]S. When you get the message, you compute the hash code h(M) and use my public key P to decrypt the signature. If the two values are the same, you can conclude that the message really came from me. Only I know my secret key S, so only I could encrypt h(M) so that it would correctly decrypt with S. As before, for this to work, you must already know and believe my public key.
An important application of digital signatures is a certificate, which is a principal's name and public key signed by another principal. Suppose Alice wants to send her public key to Bob in such a way that Bob can be reassured that it really is Alice's key. Suppose, further, that Alice and Bob have a common friend Charlie, Bob knows and trusts Charlie's public key, and Charlie knows and trusts Alice's public key. Alice can get a certificate from Charlie, which contains Alice's name and public key, and which is signed by Charlie:
[Alice + PAlice]SCharlieAlice sends this certificate to Bob. Bob verifies Charlie's signature on the certificate, and since he trusts Charlie, he believes that PAlice really is Alice's public key. He can use it to send secret messages to Alice and to verify Alice's signature on messages she sends to him. Of course, this scenario starts by assuming Bob has Charlie's public key and Charlie has Alice's public key. It doesn't explain how they got them. Perhaps they got them by exchanging other certificates, just as Bob got Alice's key. Or perhaps the keys were exchanged by some out-of-band medium such snail mail, a telephone call, or a face-to-face meeting.
A certificate authority (CA) is a service that exists expressly for the purpose of issuing certificates. When you install a web browser such as Netscape, it has built into it a set of public keys for a variety of CAs. In Netscape, click the "Security" button or select "Security info" item from the "Communicator" menu. In the window that appears, click on "Signers". You will get a list of these certificate authorities. When you visit a "secure" web page, the web server sends your browser a certificate containing its public key. If the certificate is signed by one of the CAs it recognizes, the browser generates a conventional key and uses the server's public key to transmit it securely to the server the browser and the server can now communicate securely by encrypting all their communications with the new key. The little lock-shaped icon in the lower left corner of the browser changes shape to show the lock securely closed to indicate the secure connection. Note that both public-key and conventional (private key) techniques are used. The public-key techniques are more flexible, but conventional encryption is much faster, so it is used whenever large amounts of data need to be transmitted. You can learn more about how Netscape handles security from Netscape's web site.
1A message encrypted with some other key could be "decrypted" with KA, but the results would be gibberish. The inclusion of the requests and id in the message ensures that A can tell the difference between a valid message and gibberish.