# Midterm M2B
📗 Enter your ID (the wisc email ID without @wisc.edu) here: and click 1,2,3,4,5,6,7,8,9,10 1
📗 The same ID should generate the same set of questions. Your answers are not saved when you close the browser. You could print the page: , solve the problems, then enter all your answers at the end.
📗 Please do not refresh the page: your answers will not be saved. You can save and load your answers (only fill-in-the-blank questions) using the buttons at the bottom of the page.
# Warning: please enter your ID before you start!
# Question 10
📗 [4 points] Given a linear SVM (Support Vector Machine) that perfectly classifies a set of training data containing positive examples and negative examples with 2 support vectors. After adding one more positively labeled training example and retraining the SVM, what is the maximum possible number of support vectors possible in the new SVM.
Hint
See Fall 2019 Final Q7, Fall 2019 Final Q8.📗 Answer: .
📗 [4 points] You are given a training set of five points and their 2-class classifications (+ or -): (, +), (, +), (, -), (, -), (, -). What is the decision boundary associated with this training set using 3NN (3 Nearest Neighbor)?
Hint
See Spring 2017 Midterm Q6. The decision boundary is the threshold such that all points on its left is classified as positive, and all points on its right is classified as negative. The threshold should be equidistant from the first and fourth points (i.e. the midpoint between the first and fourth points).📗 Answer: .
📗 [2 points] In a corpus with word tokens, the phrase "Fort Night" appeared times (not Fortnite). In particular, "Fort" appeared times and "Night" appeared . If we estimate probability by frequency (the maximum likelihood estimate) without smoothing, what is the estimated probability of P(Night | Fort)?
Hint
See Fall 2017 Midterm Q7, Fall 2016 Final Q4. The maximum likelihood estimate of \(\mathbb{P}\left\{B | A\right\} = \dfrac{\mathbb{P}\left\{A B\right\}}{\mathbb{P}\left\{A\right\}}\) is \(\dfrac{n_{A B}}{n_{A}}\).📗 Answer: .
📗 [4 points] Given the following transition matrix for a bigram model with words "", "" and "": . Row \(i\) column \(j\) is \(\mathbb{P}\left\{w_{t} = j | w_{t-1} = i\right\}\). What is the probability that the third word is "" given the first word is ""?
Hint
See Fall 2019 Final Q30. Sum over all possible values of the second word: \(\mathbb{P}\left\{w_{3} = j | w_{1} = i\right\} = \displaystyle\sum_{k=1}^{3} \mathbb{P}\left\{w_{3} = j | w_{2} = k\right\} \mathbb{P}\left\{w_{2} = k | w_{1} = i\right\}\), where the \(\mathbb{P}\left\{w_{t} | w_{t-1}\right\}\) probabilities are given by the transition matrix.📗 Answer: .
📗 [4 points] What is the convolution between the image and the filter using zero padding? The flipped filter is .
Hint
Use the convolution formula between matrix X and a k by k filter W that \(A_{i,j} = \displaystyle\sum_{s=-k}^{k} \displaystyle\sum_{t=-k}^{k} W_{s,t} X_{i-s,j-t}\) for every element (i,j) of the matrix X. Intuitively, flip the filter and take the dot product between the filter and the submatrix centered at each (i,j) to compute the convolution at (i,j).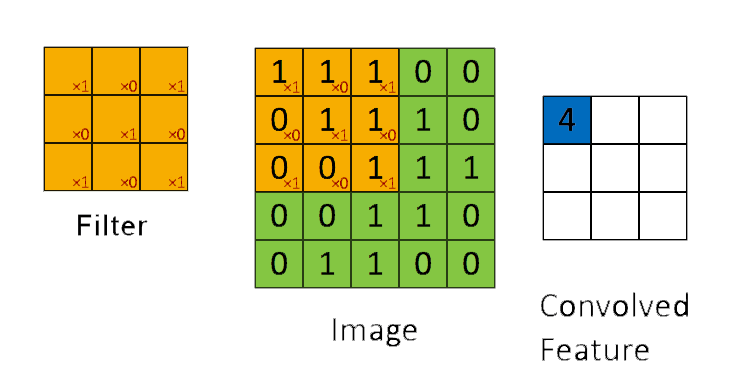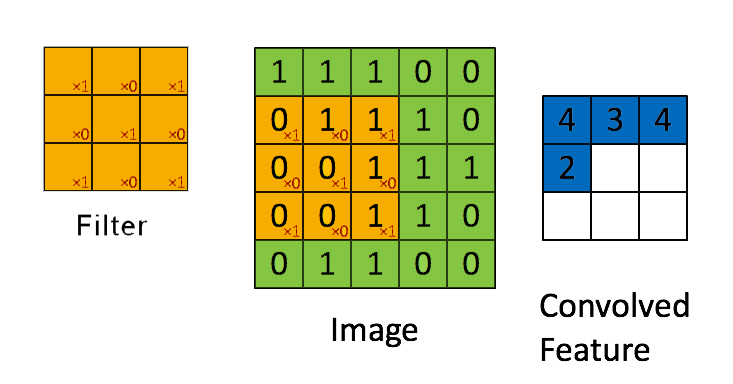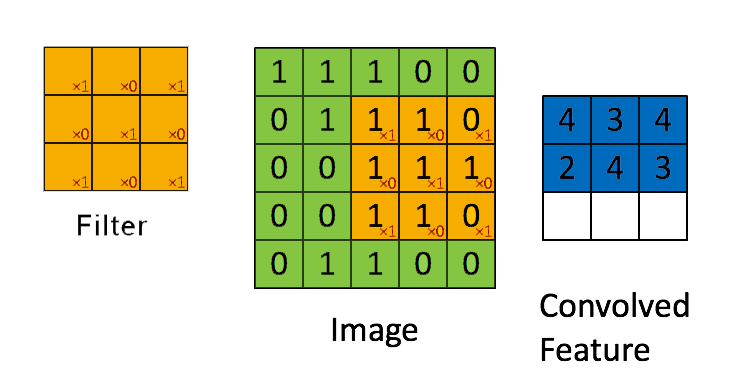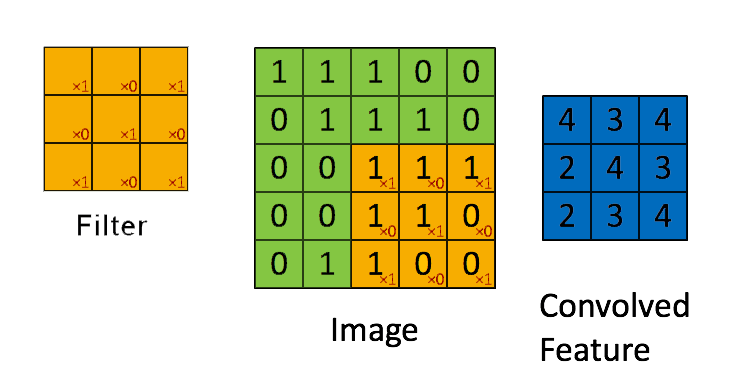
📗 Answer (matrix with multiple lines, each line is a comma separated vector): .
📗 [4 points] In a convolutional neural network, suppose the activation map of a convolution layer is . What is the activation map after a non-overlapping (stride 2) 2 by 2 average-pooling layer?
Hint
Take the maximum (or average) of each 2 by 2 submatrix and put them in a larger matrix.📗 Answer (matrix with multiple lines, each line is a comma separated vector): .
📗 [4 points] Given two items \(x_{1}\) = and \(x_{2}\) = , suppose the feature map for a kernel SVM (Support Vector Machine) is \(\varphi\left(x\right)\) = , what is the kernel (Gram) matrix?
Hint
📗 Answer (matrix with multiple lines, each line is a comma separated vector): .
📗 [3 points] A decision tree has depth \(d\) = (a decision tree where the root is a leaf node has \(d\) = 0). All its internal node have \(b\) = children. The tree is also complete, meaning all leaf nodes are at depth \(d\). If we require each leaf node to contain at least training examples, what is the minimum size of the training set?
Hint
See Fall 2014 Midterm Q9, Fall 2012 Final Q6. The total number of leaf nodes in a complete tree is \(b^{d}\), and if at least \(n\) training examples are needed in each one of them, since the same training example cannot appear in multiple subtrees, there should be at least \(n b^{d}\) training examples in total.📗 Answer: .
📗 [4 points] A convolutional neural network has input image of size x that is connected to a convolutional layer that uses a x filter, no padding of the image, and a stride of 1. There are activation maps. The convolutional layer is then connected to a pooling layer that uses x max pooling, a stride of (non-overlapping), and no padding of the convolutional layer. The pooling layer is then fully connected to an output layer that contains output units. There are no hidden layers between the pooling layer and the output layer. How many different weights must be learned in this whole network, not including any bias.
Hint
See Fall 2019 Final Q15, Spring 2018 Midterm Q8 Q9 Q10 Q11, Fall 2017 Final Q5, Spring 2017 Final Q5, Fall 2017 Midterm Q9, Fall 2017 Midterm Q11. Each k by k filter in the first layer has \(k \times k\) weights, the number of such filters depend on the number of activation maps in the next layer. The pooling layers do not have weights, but the number of units in the next layer depends on the pooling filter size (reduces the units by a factor of the filter size). The last layer is fully connected, so the number of weights is the product between the number of units in the previous layer and the number of output units.📗 Answer: .
# Warning: remember to submit this on Canvas!
📗 Please copy and paste the text between the *s (not including the *s) and submit it on Canvas, M2B.
📗 Please save a copy as text file using the button or just copy and paste it into a text file.
📗 You could load your answers using the button from the text field:
Last Updated: July 14, 2024 at 8:37 PM