Prev: L22, Next: L24
Course Links: Canvas, Piazza, TopHat (212925)
Zoom Links: MW 4:00, TR 1:00, TR 2:30.
Tools
📗 You can expand all TopHat Quizzes and Discussions: , and print the notes: , or download all text areas as text file: .
📗 For visibility, you can resize all diagrams on page to have a maximum height that is percent of the screen height: .
📗 Calculator:
📗 Canvas:
pen
# Markov Decision Process
📗 Reinforcement learning problem with multiple states is usually represented by Markov Decision Processes (MDP): Link, Wikipedia.
📗 Markov property on states and actions are assumed: \(\mathbb{P}\left\{s_{t+1} | s_{t}, a_{t}, s_{t-1}, a_{t-1}, ...\right\} = \mathbb{P}\left\{s_{t+1} | s_{t}, a_{t}\right\}\). The state in round \(t+1\), \(s_{t+1}\) only depends on the state and action in round \(t\), \(s_{t}\) and \(a_{t}\).
📗 The goal is learn a policy \(\pi\) to choose action \(\pi\left(s_{t}\right)\) that maximize the total expected discounted rewards: \(\mathbb{E}\left[r_{t} + \beta r_{t+1} + \beta^{2} r_{t+2} + ...\right]\).
➩ The reason a discount factor is used is so that the infinity sum is finite.
➩ Note that if the rewards are between \(0\) and \(1\), then the discounted total rewards is less than \(1 + \beta + \beta^{2} + ... = \dfrac{1}{1 - \beta}\).
Math Note
📗 To compute the sum, \(S = 1 + \beta + \beta^{2} + ...\), note that \(\beta S = \beta + \beta^{2} + \beta^{3} + ...\), so \(\left(1 - \beta\right) S = 1\) or \(S = \dfrac{1}{1 - \beta}\).
➩ This requires \(0 \leq \beta < 1\).
# Value Function
📗 The value function is the expected discounted reward given a policy function \(\pi\), or \(V^{\pi}\left(s_{t}\right) = \mathbb{E}\left[r_{t}\right] + \beta \mathbb{E}\left[r_{t+1}\right] + \beta^{2} \mathbb{E}\left[r_{t+2}\right] + ...\), where \(r_{t}\) is generated based on \(\pi\).
➩ To be precise, \(V^{\pi}\left(s_{t}\right) = \mathbb{E}\left[r_{t} | s_{t}, \pi\right] + \beta \mathbb{E}\left[r_{t+1} | s_{t}, \pi\right] + \beta^{2} \mathbb{E}\left[r_{t+2} | s_{t}, \pi\right] + ...\).
📗 The value function is the (only) function that satisfies the Bellman's equation: \(V^{\pi}\left(s_{t}\right) = \mathbb{E}\left[r_{t} | s_{t}, \pi\right] + \beta \mathbb{E}\left[V^{\pi}\left(s_{t+1}\right) | s_{t}, \pi\right]\).
📗 The optimal policy \(\pi^\star\) is the policy that maximizes the value function at every state.
# Q Function
📗 The Q function is the value function given a specific action in the current period (and follows \(\pi\) in future periods).
➩ By definition, \(Q^{\pi}\left(s_{t}, a_{t}\right) = \mathbb{E}\left[r_{t} | s_{t}, a_{t}\right] + \beta \mathbb{E}\left[r_{t+1} | s_{t}, a_{t}, \pi\right] + \beta^{2} \mathbb{E}\left[r_{t+2} | s_{t}, a_{t}, \pi\right] + ...\), which can be written as \(Q^{\pi}\left(s_{t}, a_{t}\right) = \mathbb{E}\left[r_{t} | s_{t}, a_{t}\right] + \beta \mathbb{E}\left[V^{\pi}\left(s_{t+1}\right) | s_{t}, a_{t}, \pi\right]\).
📗 Under the optimal policy, the Bellman's equation is satisfied: \(Q^\star\left(s_{t}, a_{t}\right) = \mathbb{E}\left[r_{t} | s_{t}, a_{t}\right] + \beta \mathbb{E}\left[V^\star\left(s_{t+1}\right) | s_{t}, a_{t}\right]\), for every state and action, where \(V^\star\left(s_{t+1}\right) = \displaystyle\max_{a} Q^\star\left(s_{t+1}, a\right)\).
📗 Bellman's equation can be used to iteratively solve for the Q function:
➩ Initialize \(\hat{Q}\left(s_{t}, a_{t}\right)\) for every state and action.
➩ Update \(\hat{Q}\left(s_{t}, a_{t}\right) \leftarrow \mathbb{E}\left[r_{t} | s_{t}, a_{t}\right] + \beta \mathbb{E}\left[\displaystyle\max_{a} \hat{Q}\left(s_{t+1}, a\right)\right]\).
➩ \(\hat{Q}\) converges to \(Q^\star\) given any initialization, assuming \(0 \leq \beta < 1\).
TopHat Discussion
ID:📗 [1 points] Compute the optimal policy (at each state the car can go Up, Down, Left, Right, or Stay). The color represents the reward from moving to each state (more red means more negative and more blue means more positive). Click on the plot on the right to update the Q function once. The discount factor is .
📗 Q Function (columns are U, D, L, R, S):
📗 V Function:
📗 Policy:
TopHat Quiz
(Past Exam Question) ID:📗 [4 points] Consider the following Markov Decision Process. It has two states \(s\), A and B. It has two actions \(a\): move and stay. The state transition is deterministic: "move" moves to the other state, while "stay" stays at the current state. The reward \(r\) is for move (from A and B), for stay (in A and B). Suppose the discount rate is \(\beta\) = .
Find the Q function in the format described by the following table. Enter a two by two matrix.
| State \ Action | stay | move |
| A | ? | ? |
| B | ? | ? |
📗 Answer (matrix with multiple lines, each line is a comma separated vector): .
# Q Learning
📗 The Q function can be learned by iteratively update the Q function using the Bellman's equation: Link, Wikipedia.
➩ \(\hat{Q}\left(s_{t}, a_{t}\right) = \left(1 - \alpha\right) \hat{Q}\left(s_{t}, a_{t}\right) + \alpha \left(r_{t} + \beta \displaystyle\max_{a} \hat{Q}\left(s_{t+1}, a\right)\right)\), where \(\alpha\) is the learning rate and is sometimes set to \(\dfrac{1}{1 + n\left(s_{t}, a_{t}\right)}\), \(n\left(s_{t}, a_{t}\right)\) is the number of visits to state \(s_{t}\) and action \(a_{t}\) in the past.
📗 Under certain assumptions, Q learning converges to the correct (optimal) Q function, and the optimal policy can be obtained by: \(\pi\left(s_{t}\right) = \mathop{\mathrm{argmax}}_{a} Q^\star\left(s_{t}, a\right)\) for every state.
TopHat Discussion
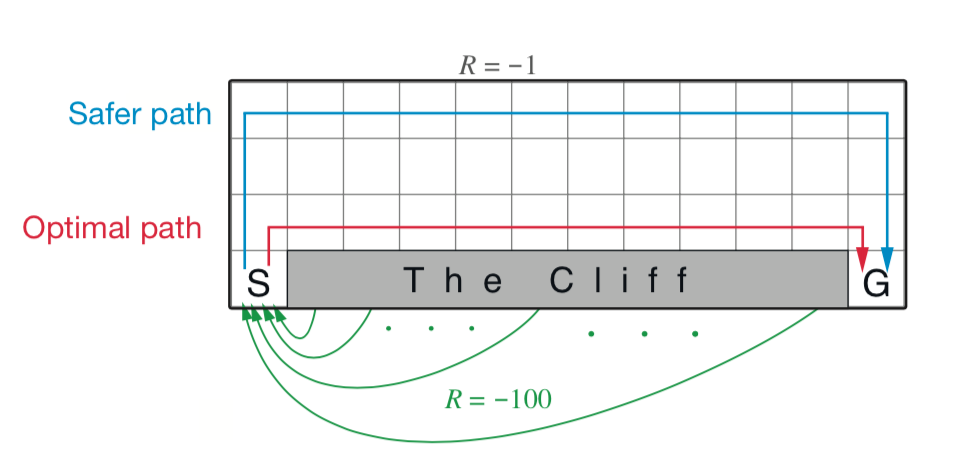
📗 [1 points] Compute the optimal policy (at each state the agent can go Up, Down, Left, Right). Falling into the cliff (black) leads to a loss of \(-100\) and walking (white) anywhere else leads to a loss of \(-1\). The agent starts at the blue tile and stops at the green tile.
📗 Click on the plot on the left to update the Q function times using Q learning. The plot on the right shows the number of visits to each square.
Epsilon greedy: \(\varepsilon\) = 0.1
Learning rate: \(\alpha\) = 0.1 or use \(\alpha = \dfrac{1}{1+n}\)
📗 Q Function (columns are U, D, L, R):
📗 V Function:
📗 Policy:
# SARSA
📗 An alternative to Q learning is SARSA (State Action Reward State Action). It uses a pre-specified action for the next period instead of the optimal action based on the current Q estimate: Wikipedia.
➩ \(\hat{Q}\left(s_{t}, a_{t}\right) = \left(1 - \alpha\right) \hat{Q}\left(s_{t}, a_{t}\right) + \alpha \left(r_{t} + \beta \hat{Q}\left(s_{t+1}, a_{t+1}\right)\right)\).
📗 The main difference is the action used in state \(s_{t+1}\).
➩ Q learning is an off-policy learning algorithm since \(a_{t+1}\) is the optimal policy in the next period, not a pre-specified policy (the Q function during learning does not correspond to any policy).
➩ SARSA is an on-policy learning algorithm since it computes the Q function based on a fixed policy.
TopHat Discussion
📗 [1 points] Compute the optimal policy (at each state the agent can go Up, Down, Left, Right). Falling into the cliff (black) leads to a loss of \(-100\) and walking (white) anywhere else leads to a loss of \(-1\). The agent starts at the blue tile and stops at the green tile.
📗 Click on the plot on the left to update the Q function times using Q learning. The plot on the right shows the number of visits to each square.
Epsilon greedy: \(\varepsilon\) = 0.1
Learning rate: \(\alpha\) = 0.1 or use \(\alpha = \dfrac{1}{1+n}\)
📗 Q Function (columns are U, D, L, R):
📗 V Function:
📗 Policy:

# Exploration vs Exploitation
📗 The policy used to generate the data for Q learning or SARSA can be Epsilon Greedy or UCB (requires some modification for MDPs).
➩ Epsilon greedy: with probability \(\varepsilon\), \(a_{t}\) is chosen uniformly randomly among all actions; with probability \(1-\varepsilon\), \(a_{t} = \mathop{\mathrm{argmax}}_{a} \hat{Q}\left(s_{t}, a\right)\).
📗 The choice of action can be randomized too: \(\mathbb{P}\left\{a_{t} | s_{t}\right\} = \dfrac{c^{\hat{Q}\left(s_{t}, a_{t}\right)}}{c^{\hat{Q}\left(s_{t}, 1\right)} + c^{\hat{Q}\left(s_{t}, 2\right)} + ... + c^{\hat{Q}\left(s_{t}, K\right)}}\), where \(c\) is a parameter controlling the trade-off between exploration and exploitation.
test car,ql,qcl,scl q
📗 Notes and code adapted from the course taught by Professors Jerry Zhu, Yingyu Liang, and Charles Dyer.
📗 Content from note blocks marked "optional" and content from Wikipedia and other demo links are helpful for understanding the materials, but will not be explicitly tested on the exams.
📗 Please use Ctrl+F5 or Shift+F5 or Shift+Command+R or Incognito mode or Private Browsing to refresh the cached JavaScript.
📗 You can expand all TopHat Quizzes and Discussions: , and print the notes: , or download all text areas as text file: .
📗 If there is an issue with TopHat during the lectures, please submit your answers on paper (include your Wisc ID and answers) or this Google form Link at the end of the lecture.
📗 Anonymous feedback can be submitted to: Form.
Prev: L22, Next: L24
Last Updated: January 19, 2026 at 9:18 PM