Prev: L23, Next: L25
Course Links: Canvas, Piazza, TopHat (212925)
Zoom Links: MW 4:00, TR 1:00, TR 2:30.
Tools
📗 You can expand all TopHat Quizzes and Discussions: , and print the notes: , or download all text areas as text file: .
📗 For visibility, you can resize all diagrams on page to have a maximum height that is percent of the screen height: .
📗 Calculator:
📗 Canvas:


Slide:

# The materials covered in this lecture will not be on the exams.




# Deep Q Learning

📗 In practice, Q function stored as a table is too large if the number of states is large or infinite (the action space is usually finite): Link, Link, Wikipedia.
📗 If there are \(m\) binary features that represent the state, then the Q table contains \(2^{m} \left| A \right|\), which can be intractable.
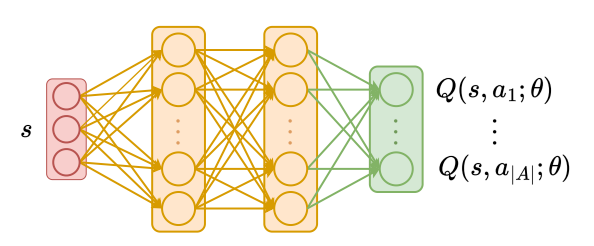
📗 In this case, a neural network can be used to store the Q function, and if there is a single layer with \(m\) units, then only \(m^{2} + m \left| A \right|\) weights are needed.
➩ The input of the network \(\hat{Q}\) is the features of the state \(s\), and the outputs of the network are Q values associated with the actions \(a\) or \(Q\left(s, a\right)\) (the output layer does not need to be softmax since the Q values for different actions do not need to sum up to \(1\)).
➩ After every iteration, the network can be updated based on an item \(\left(s_{t}, \left(1 - \alpha\right) \hat{Q}\left(s_{t}, a_{t}\right) + \alpha \left(r_{t} + \beta \displaystyle\max_{a} \hat{Q}\left(s_{t+1}, a\right)\right)\right)\).



# Deep Q Network

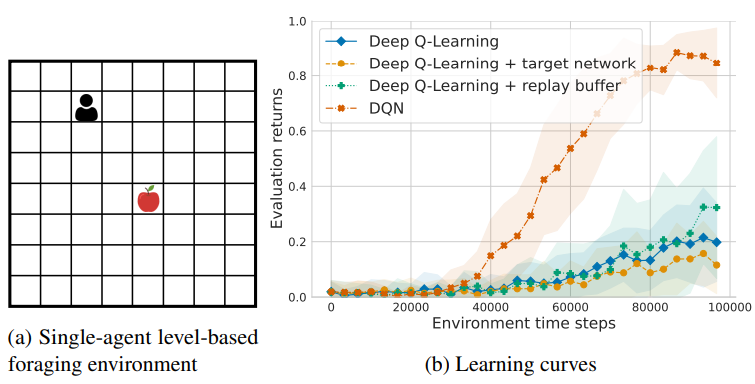
📗 Deep Q Learning algorithm is unstable since the training label uses the network itself. The following improvements can be made to make the algorithm more stable, called DQN (Deep Q Network).
➩ Target network: two networks can be used, the Q network \(\hat{Q}\) and the target network \(Q'\), and the new item for training \(\hat{Q}\) can be changed to \(\left(s_{t}, \left(1 - \alpha\right) Q'\left(s_{t}, a_{t}\right) + \alpha \left(r_{t} + \beta \displaystyle\max_{a} Q'\left(s_{t+1}, a\right)\right)\right)\).
➩ Experience replay: some training data can be saved and a mini-batch (sampled from the training set) can be used to update \(\hat{Q}\) instead of a single item.
Example
DQN
DQN Plot



# Policy Gradient

📗 Deep Q Network estimates the Q function as a neural network, and the policy can be computed as \(\pi\left(s\right) = \mathop{\mathrm{argmax}}_{a} \hat{Q}\left(s, a\right)\), which is always deterministic.
➩ In single-agent reinforcement learning, there is always a deterministic optimal policy, so DQN can be used to solve for an optimal policy.
➩ In multi-agent reinforcement learning, the optimal equilibrium policy can be all stochastic (mixed strategy equilibrium): Wikipedia.
📗 The policy can also be represented by a neural network called the policy network \(\hat{\pi}\) and it can be trained with or without using a value network \(\hat{V}\).
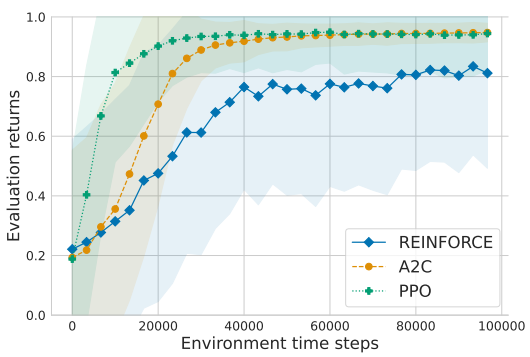
➩ Without a value network: REINFORCE (REward Increment = Non-negative Factor x Offset x Characteristic Eligibility).
➩ With a value network: A2C (Advantage Actor Critic) and PPO (Proximal Policy Optimization).
📗 To train the policy network \(\hat{\pi}\), the input is the features of the state \(s\) and the output units (softmax output layer) are the probability of using each action \(a\) or \(\mathbb{P}\left\{\pi\left(s\right) = a\right\}\). The cost function the network minimizes can be value function (REINFORCE) or the advantage function (difference between value and Q, A2C and PPO).
📗 The value network is trained in a way similar to DQN.
Example
A2C
Math Note (Optional)
📗 Policy gradient theorem: \(\nabla_{w} V\left(w\right) = \mathbb{E}\left[Q^{\hat{\pi}}\left(s, a\right) \nabla_{w} \log \hat{\pi}\left(a | s; w\right)\right]\)
➩ Given this gradient formula, the loss for the policy network in REINFORCE can be written as \(\left(\displaystyle\sum_{t'=t+1}^{T} \beta^{t'-t-1} r_{t'}\right) \log \pi\left(a_{t} | s_{t} ; w\right)\), where \(\displaystyle\sum_{t'=t+1}^{T} \beta^{t'-t-1} r_{t'}\) is an estimate of \(Q^{\hat{\pi}}\left(s_{t}, a_{t}\right)\).
➩ The loss for the policy network in A2C is \(-\left(r_{t} + \beta \hat{V}\left(s_{t+1}\right) - \hat{V}\left(s_{t}\right)\right) \log \pi\left(a_{t} | s_{t} ; w\right)\), where \(r_{t} + \beta \hat{V}\left(s_{t+1}\right) - \hat{V}\left(s_{t}\right)\) is an estimate of the advantage function \(Q^{\hat{\pi}}\left(s_{t}, a_{t}\right) - V^{\hat{\pi}}\left(s_{t}\right)\).



📗 Notes and code adapted from the course taught by Professors Jerry Zhu, Yingyu Liang, and Charles Dyer.
📗 Content from note blocks marked "optional" and content from Wikipedia and other demo links are helpful for understanding the materials, but will not be explicitly tested on the exams.
📗 Please use Ctrl+F5 or Shift+F5 or Shift+Command+R or Incognito mode or Private Browsing to refresh the cached JavaScript.
📗 You can expand all TopHat Quizzes and Discussions: , and print the notes: , or download all text areas as text file: .
📗 If there is an issue with TopHat during the lectures, please submit your answers on paper (include your Wisc ID and answers) or this Google form Link at the end of the lecture.
📗 Anonymous feedback can be submitted to: Form.

Prev: L23, Next: L25





Last Updated: February 06, 2025 at 2:57 AM