📗 [4 points] Given a linear SVM (Support Vector Machine) that perfectly classifies a set of training data containing positive examples and negative examples. What is the maximum possible number of training examples that could be removed and still produce the exact same SVM as derived for the original training set?

Hint

See Fall 2019 Final Q7 Q8.

📗 Answer: .

📗 [3 points] What is the minimum zero-one cost of a binary (y is either 0 or 1) linear (threshold) classifier (for example, LTU perceptron) on the following data set?


📗 A linear classifier is a vertical line that separates the two classes: you want to draw the line such that the least number of mistakes (i.e. zero-one cost) are made.

Hint

The zero-one cost is \(C = \displaystyle\min_{b} \displaystyle\sum_{i=1}^{n} 1_{\left\{\hat{y}_{i} \neq y_{i}\right\}}\), where \(\hat{y}_{i}\) is the prediction of the classifier. A linear classifier with threshold \(t\) is either in form (1) \(\hat{y}_{i} = 0\) when \(x_{i} \leq t\) and \(\hat{y}_{i} = 1\) when \(x_{i} > t\) or (2) \(\hat{y}_{i} = 1\) when \(x_{i} \leq t\) and \(\hat{y}_{i} = 0\) when \(x_{i} > t\). For this question, you can try \(t = 0, 1, 2, 3, 4, 5, 6, 7\) and check which one leads to the smallest zero-one cost.

📗 Answer: . Calculate

📗 [4 points] You are given a training set of five points and their 2-class classifications (+ or -): (, +), (, +), (, -), (, -), (, -). What is the decision boundary associated with this training set using 3NN (3 Nearest Neighbor)?

Hint

See Spring 2017 Midterm Q6. The decision boundary is the threshold such that all points on its left is classified as positive, and all points on its right is classified as negative. The threshold should be equidistant from the first and fourth points (i.e. the midpoint between the first and fourth points).

📗 Answer: . Calculate

📗 [4 points] Given the following transition matrix for a bigram model with words "", "" and "": . Row \(i\) column \(j\) is \(\mathbb{P}\left\{w_{t} = j | w_{t-1} = i\right\}\). What is the probability that the third word is "" given the first word is ""?

Hint

See Fall 2019 Final Q30. Sum over all possible values of the second word: \(\mathbb{P}\left\{w_{3} = j | w_{1} = i\right\} = \displaystyle\sum_{k=1}^{3} \mathbb{P}\left\{w_{3} = j | w_{2} = k\right\} \mathbb{P}\left\{w_{2} = k | w_{1} = i\right\}\), where the \(\mathbb{P}\left\{w_{t} | w_{t-1}\right\}\) probabilities are given by the transition matrix.

📗 Answer: . Calculate

📗 [4 points] What is the convolution between the image and the filter using zero padding? Remember to flip the filter first.

Hint

Use the convolution formula between matrix X and a k by k filter W that \(A_{i,j} = \displaystyle\sum_{s=-k}^{k} \displaystyle\sum_{t=-k}^{k} W_{s,t} X_{i-s,j-t}\) for every element (i,j) of the matrix X. Intuitively, flip the filter and take the dot product between the filter and the submatrix centered at each (i,j) to compute the convolution at (i,j).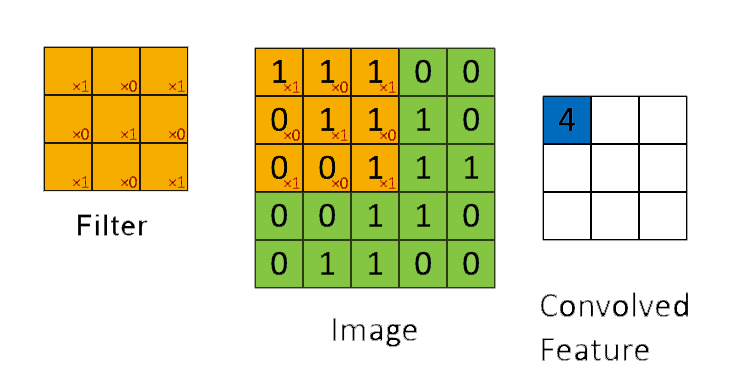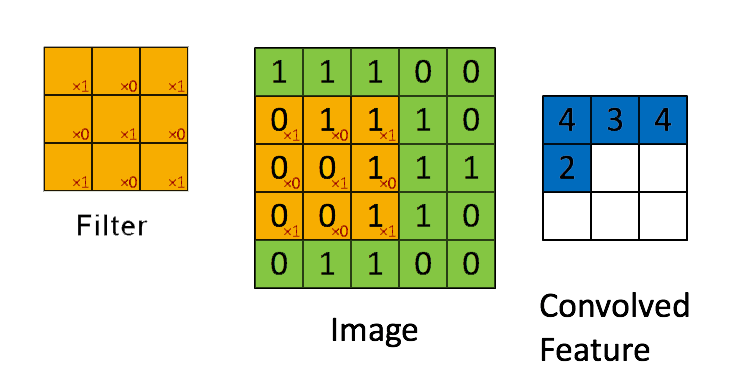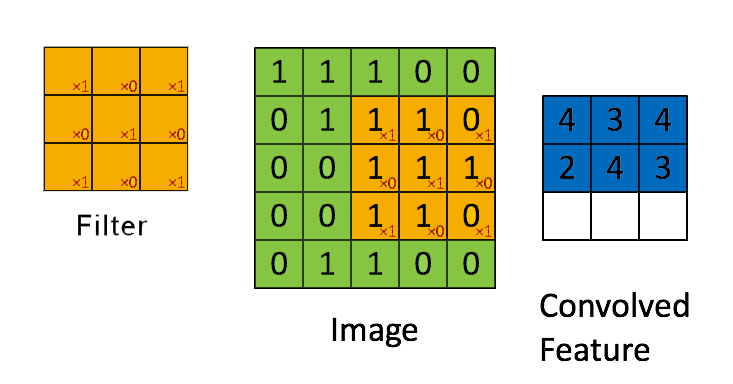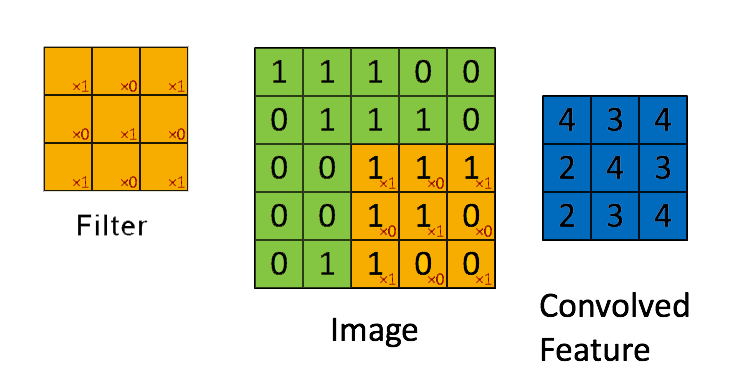

📗 Answer (matrix with multiple lines, each line is a comma separated vector): . Calculate

📗 [4 points] If \(\mathbb{P}\left\{A | B\right\}\) is times the value of \(\mathbb{P}\left\{B | A\right\}\), and \(\mathbb{P}\left\{A\right\}\) = . What is \(\mathbb{P}\left\{B\right\}\)?

Hint

See Fall 2013 Final Q11, Fall 2012 Midterm Q9, Fall 2011 Midterm Q14.

📗 Answer: . Calculate

📗 [4 points] Given two instances \(x_{1}\) = and \(x_{2}\) = , suppose the feature map for a kernel SVM (Support Vector Machine) is \(\varphi\left(x\right)\) = , what is the kernel (Gram) matrix?

Hint

📗 Answer (matrix with multiple lines, each line is a comma separated vector): . Calculate

📗 [4 points] Say we use Naive Bayes in an application where there are features represented by variables, each having possible values, and there are classes. How many probabilities must be stored in the CPTs (Conditional Probability Table) in the Bayesian network for this problem? Do not include probabilities that can be computed from other probabilities.

Hint

See Fall 2019 Final Q27.

📗 Answer: . Calculate

📗 [4 points] A convolutional neural network has input image of size x that is connected to a convolutional layer that uses a x filter, no padding of the image, and a stride of 1. There are activation maps. The convolutional layer is then connected to a pooling layer that uses x max pooling, a stride of (non-overlapping), and no padding of the convolutional layer. The pooling layer is then fully connected to an output layer that contains output units. There are no hidden layers between the pooling layer and the output layer. How many different weights must be learned in this whole network, not including any bias.

Hint

See Fall 2019 Final Q15, Spring 2018 Midterm Q8 Q9 Q10 Q11, Fall 2017 Final Q5, Spring 2017 Final Q5, Fall 2017 Midterm Q9, Fall 2017 Midterm Q11. Each k by k filter in the first layer has \(k \times k\) weights, the number of such filters depend on the number of activation maps in the next layer. The pooling layers do not have weights, but the number of units in the next layer depends on the pooling filter size (reduces the units by a factor of the filter size). The last layer is fully connected, so the number of weights is the product between the number of units in the previous layer and the number of output units.

📗 Answer: . Calculate

📗 [1 points] Please enter any comments including possible mistakes and bugs with the questions or your answers. If you have no comments, please enter "None": do not leave it blank.
📗 Answer: .