Uncalibrated Stereo Vision
0. Project Information
Project Title: Uncalibrated Stereo Vision
Course: CS 766, University of Wisconsin, - Madison
Authors: Tom Brunet and Leo Chao
Contents
Given a series of two-dimensional images it is possible to extract a significant amount of auxillary information
about the scene being captured. One of the most useful of these pieces of information is knowledge about the
relative depth of objects in the scene. It is known that, given two images of a single scene it is possible to
extract the depth of various objects in the scene from the disparity between the two images. The human brain handles
this task constantly, adapting a stream of paired two dimensional images to provide us with what is commmonly known as
depth perception: that is a instrinsic feel for the relative depth of objects in the scene. In a much simpler case we can
consider how to extract this scene disparity from two images viewing the same scene (from close but not identitcal positions).
It should be noted that without a significant amount of extra information and calculations, it is generally not possible to
ascertain an exact depth measurement (as in so many meters out) but rather we can isolate "planes" of depth, that is localize which
parts of the scene are at the same, or relatively close, depths.
Being able to retrive this depth information is useful for any number of applications. Most prominent of these are 3D scene reconstruction,
where the depth information is used to aid in the creation of a three-dimensional model of the scene being captured. Similarly,
robotics applications often use a rough 3D scene model garnered from a stereo rig to model the world around a robot in order to provide
sane movement and navigation data to the machine. In general these stereo vision techniques are desireable because they are passive in nature,
that is no active measurements of the scene with instruments such as radar or lasers need to be obtained. Furthermore their exist a significant
range of processes which enable a user to either process the data offline, or in real-time, as the application dictates.
In order to obtain the desired depth information we need to first determine the disparity between the two images. Traditionally these two images
are referred to as the left and right images. Since the left and right images are viewing the plane from different place, there will be a noticeable
disparity between the two images. If we are able to calculate the relative disparity between points in a scene across the two different images we should
be able to create a depth map from that information. The vital point here is that points at similar depth levels in the world will have similar disparities
across the left and right stereo images. Intuitively this can be seen just by moving ones head laterally: objects close to you move a large distance in your
field of view while those further away move a small distance. By determining a displacement for each point in an image, we can determine roughly which depth
layer it belongs to. Thus given a set of point correspondences between the left and right images, we can determine the depth map of the scene.
Fundamental to the calculation of these point correspondences, is the idea of an epipolar plane. Essentially this is a technique for constraining the search space when
looking for corresponding points between the left and right images. Simply put the epipolar plane is the plane formed by the point in the scene and the optical centers
of the left and right cameras. Where this plane intersects the two image planes an epipolar line is formed on each image plane. This is the line that joins the image
of the scene point in each of the images to the epipole in each image. The epipoles are the point in each image where the line between the two optical centers
intersectst he image plane. The figure below demonstrates these terms. [ref: Epipolar Geometry]
This approach assumes that we know the parameters for the stereo rig and reduce our search for correspondences to the epipolar lines. The key features of this type of correspondence
processing is that the epipolar lines are easily determine, since camera parameters are known and the emphasis is on increasing the speed and accuracy of the search itself. There are
a wide variety of approaches to solving this problem, Scharstein and Szeliski provide a good overview of the general
methods and approaches as well as characterizing the performance of each. The key features that differentiate these algorithms is the calculation of match costs, the means in which costs
are aggregated, the actual disparity calcualtions used and the amount of refinement the disparity levels are subject to. Of thse, the key structure differences generally lie in the
disparity calculation section where techniquies such as local window searches, global cost optimization and dynamic programming routines are used to efficiently (or not so) search the epipolar
lines for desired matches.
For the purposes of our project we treat this part as a black-box, since we know there exist a number of useful algoritms for doing this task. We use the implementation in openCV which is
based on the Birchfield and Tomasi algorithm that employs dynamic programming to find the
correspondences. We note here that the input to all these algorithms is assumed to be a pair of rectified, that is calibrated images. Since we are dealing with the uncalibrated case we
need to be able to rectify these images so that they lie parallel to one another in order to make use of these algorithms.
Like the calibrated case, the goal here is the narrow the search space enough so that we can determine good correspondences between points in the left and right images. Unlike the calibrated
case this is no longer a simple task of search along the epipolar lines to correspondence (insofar as that was considered simple). Since we no longer know the camera calibration parameters
assoicated with the image pair, we can no longer easily find the epipolar lines. In order to compute the correspondences using the calibrated stereo methods we must some how rectify our
two images into the same image space. Since it is known that the two cameras are viewing the same scene we can assume that the two points, p1 and p2, can be modifed by a calibration matrix, K,
into two points, p1* and p2* (that is p1* = K p1 and p2* = K p2). Since the calibrated equations work for the points p1* and p2* (K is a calibration matrix) we can then state that transpose(p1*) F p2*
= 0 where F is the essential matrix E (which represents the epipolar lines and is used in calibrated correspondence) modified by K as F = inverse_transpose(K) E inverse(K). Since F is defined up
to scale and is a 3x3 matrix, we can detemine what F is, and thus what our epipolar lines are, if we have eight known corresponding points. This process of determineing the fundamental matrix using
a set of known corrspondence is known as the weak calibration method and is widely used to determine a fundamental matrix which can then be used to find epipolar lines. These lines can then be used
in pre-existing algorithms by rectifing the stereo images so that the scan lines are the epipolar lines as well.
In our project we use the weak calibration method to attempt to determine a fundamental matrix, rectify the image, and use the existing openCV stereo correspondence algorithm to compute the depth maps.
In our approach we attempt to implement an iterative weak calibration stereo correspondence system for determining a depth map given uncalibrated stereo images. Our approach relies on
a feature tracker to determine some initial correspondences. Currently we use KLT but have determined that it is very bad at locating feature corresponences. The pipeline goes as follows:
0 - Find Correspondence using the KLT feature point tracker.
Note that we only rely on the original feature point tracker to give us okay results, but we are uncertain how much the iterate-and-search-for-close-points approach will help if we are given
extemely errornous correspondences from the tracker.
Step 0
Step 1
Step 2
We would ideally like a relationship between the desired transform and the fundamental matrix. It is clearly a possible mapping since the goal of the transform is to map epipolar lines to
the scanlines of the images and the fundamental matrix allows us to characterize out epipolar lines. A paper out of Microsoft by
Loop and Zhang present a means of determining rectification homographies from the fundamental matrix by solving for the projective, similarlity and shearing transforms separately. Distortion
minimization techniques were applied to the projective step in order obtain cleaner homographies. The outcome of this procedure was a pair of images rectified into the same viewspace where
the epipolar lines were parallel.
Step 3
Step 4
0. Project Information
1. Introduction
2. Calibrated Stereo Correspondence
3. Uncalibrated Stereo Correspondence
4. Our Approach
1. Introduction
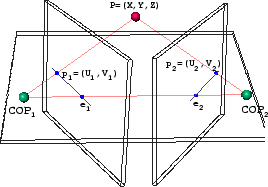
Ideally the point in the right image corresponding to any given point in the left image is known then to lie on the epipolar line in the right image that is associated with the point in the left.
We can then merely search along the line to find the proper correspondence. This ideal case is the calibrated stereo correspondence case where the parameters of the stereo rig are known. In
our project we attempt to deal with the case where these parameters are not known, that is we seek to perform stereo correspondence on two images without knowledge of their parameters.
This is known as the uncalibrated stereo correspondence problem.
2. Calibrated Stereo Correspondence
3. Uncalibrated Stereo Correspondence
4. Our Approach
1 - Determine the Fundamental Matrix, F.
2 - Recify images using F.
3 - Apply Birchfield and Tomasi calibated stereo correspondence algorithm to create a depth map.
4 - If the depth map generated is bad, determine new correspondence points by searching the space near the epipolar lines determined originally.
5 - Repeat from step 1, using the new correspondence points.
As the weak calibration method requires there to be a set of known correspondences before hand in order to calculate the fundamantal matrix, we were faced with a choice. Either we could
determine points by hand, manually finding 8 corresponding points, or we could use a feature tracker to attempt to find eight decent correspondences directly from the image information. We
picked the second approach and used the KLT feature tracker.
Given the corresponding points we are able to use this:

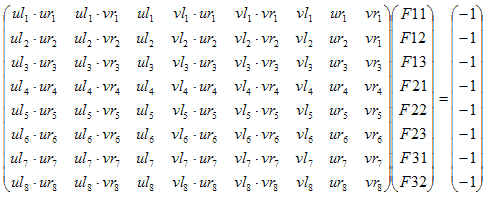
Since it is known that the fundamental matrix is the essential matrix, modified by the camera calibration parameters, it is possible to rectify the two images into a common image space given
enough knowledge of the camera parameters. Unfortunately in the uncalibrated case we have very little knowledge of camera parameters, essentially the only information we have must be obtained
from the images themselves. There exist a number of algorithms to calculate the desired transform matricies for the images based on knowedge of some of these camera parameters, but none of these
are really useful in our case since we simply do not have enough information about the cameras involved.
Once given a pair of rectified images we pass these images into a calibrated stereo correspondence algorithm. In our case we use the dynamic programming approach presented by
Birchfield and Tomasi. Essentially this algorithm assumes a pair of rectified images and
then searches the epipoles, which are the scanlines, in the right image for matches to points in the left image. Once these matches are found a displacement map is created that shows
how far each point in the left image moved when matched to its corresponding point in the right image. From this a depth map can be created by assigning points with similar disparities
to the same depth layers. The implementation is a part of openCV.
Once a depth map is generated the results can be analyzed to determine if it is a good depth mapping or not. Analysis could ideally be automatic, but a human visual scan is sufficient. If the
depth map is considered sufficient, then it is the final result. Otherwise we must determine a new set of corresponding points in the right image. Ideally we would search near the epipolar
line in the right image (corresponding to the desired point in the left image) to find another good match. Do this for all eight points in the left image and run the algorithm again for the
new matches.