
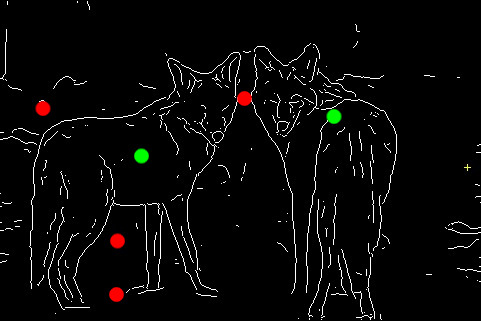


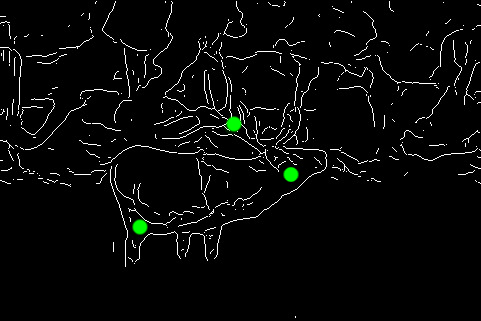

Abstract
We study the problem of interactive segmentation and contour completion for multiple objects. The form of constraints our model incorporates are those coming from user scribbles (interior or exterior constraints) as well as information regarding the topology of the 2-D space after partitioning (number of closed contours desired). We discuss how concepts from discrete calculus and a simple identity using the Euler characteristic of a planar graph can be utilized to derive a practical algorithm for this problem. We also present specialized branch and bound methods for the case of single contour completion under such constraints. On an extensive dataset of ~1000 images, our experiments suggest that a small amount of side knowledge can give strong improvements over fully unsupervised contour completion methods. We show that by interpreting user indications topologically, user effort is substantially reduced.