Exercises

Please complete each exercise or answer the question before reviewing the posted solution comments.

1. You are working with a tank that has a radius that varies by height according to the following relationship (all measurements in feet):

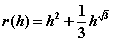
   We can find the volume of a container with varying radius by using the following expression:

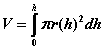
   Therefore, the integral we need to evaluate to find the volume of a tank that is H feet high and a radius that is a function of height according to r(h) above, is:

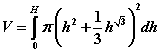
   Use Matlab to determine the volume (evaluate the integral) for such a tank that is 5 feet high:

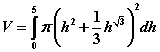
   First, define a function that returns the cross-sectional area of the tank at a specified height.

             function xarea = tank_cross_section(h)
             % Returns the cross-sectional area of a tank
             xarea = pi*(h.^2+(1/3)*h.^sqrt(3)).^2;
           

   Notice the periods, this is so that the function still will work when a matrix is passed to it. This allows the integral function to have the function evaluate more than one value at a time. This ability is required for integral to correctly determine the result.

   Compute the value by typing:

             >> integral(@tank_cross_section,0,5)
           

   Matlab will return with ans = 2.9652e+003 In other words, our tank volume is 2965.2 cubic feet. Remember, if you plan to use this value again, name it (such as TVol = integral(@tank,0,5). That way, TVol = 2965.2)

   Note: Although it is good programming practice to define the function in a separate M-file, the integral function can be executed with an anonymous function:

             >> TVol = integral(@(h)pi*(h.^2+(1/3)*h.^sqrt(3)).^2,0,5)