The INTEGRAL Function

The integral function numerically integrates a function using an adaptive quadrature approximation. You must define a function that works for vector inputs and pass that function (as a function handle) to the integral function.

To use the integral function, you also pass the limits of integration that the function will use. Here's an example that returns the area under the curve defined in my_function.m over the range from a to b:

    >> integral( @my_function, 0, 10 )

Be sure to use element-wise (dot) operators in the function definition so that it will be evaluated correctly for vector input.

If your function requires additional constant input values, you will need to use a parameter for the constant and a different syntax. This is the same syntax used if additional parameters are required when using fzero. For example, to use integral to evaluate this function 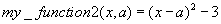for different values of a, like 5 or 8:

    >> Q = integral( @(x)my_function2(x,5) , 0 , 2 );

    >> Q = integral( @(x)my_function2(x,8) , 0 , 2 );

The my_function2 function is defined as follows:

    function y = my_function2( x , a )
    y = (x - a).^2 - 3;