Examples

1. Use the Command Window to evaluate 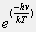for k=0.42, T=13.7 and hv=2.54.

        >> hv=2.54;
        >> T=13.7;
        >> k=0.42;
        >> result=exp(-hv/(k*T))
   
        result =
   
          0.6431

   Note the use of the built-in exponential function exp and that the variables had to be assigned be first.

2. The size function returns a vector with the number of rows as the first element and the number of columns as the second element. For example, the following shows the commands (as well as the Matlab output) to create a 3 x 4 matrix named A and a 6 x 1 matrix named V and then uses the size() function to show the dimensions (rows and columns) of A and V:

        >> A = [1 2 3 4; 5 6 7 8; 9 10 11 12];
        >> V = [10 : -2 : 0]';
        >> size(A)
        
        ans =
        
            3     4
            
        >> size(V)
        
        ans =
        
            6     1

   Notice that the first element in the array returned by size is the number of rows in the input matrix. The second element in the array is the number of columns in the input matrix.

   Did you notice that V is a column vector and not a row vector? This is because of the use of the transpose operator ('). This is a common technique when you need a column vector but would still like use the colon operator (:) to auto-generate the values of a vector.

3. The length() function is ideally suited for vectors (single-dimension arrays), as it returns the larger value of the number of rows and number of columns. It returns the number of items in the vector. Continuing our example from above, we get:

        >> length(A)
   
        ans =
        
            4
            
        >> length(V)
        
        ans = 
        
            6

   Note that the value that is returned by length() is the larger of the two dimensions of the array.

   Matlab has several dozen functions that you can use to create matrices. For the most part, it is not worth memorizing the specifics of how to use each of these functions since there are many that you will rarely, if ever, use and you can use Matlab's help facilities to find out about the ones you are interested in.

4. The diag() function will put a vector of values as the values along the diagonal of a matrix. Type the following and press enter to see the matrix that is created.

       >> A = diag( [2 3 4 5] )
       >> B = diag( -3:3 )

   >> diag( [2 3 4 5] )
   
   ans =
   
        2     0     0     0
        0     3     0     0
        0     0     4     0
        0     0     0     5
   
   >> diag( -3:3 )
   
   ans =
   
       -3     0     0     0     0     0     0
        0    -2     0     0     0     0     0
        0     0    -1     0     0     0     0
        0     0     0     0     0     0     0
        0     0     0     0     1     0     0
        0     0     0     0     0     2     0
        0     0     0     0     0     0     3
   >> 
   

   Are the matrices what you expected? The input to the diag() function is a vector that contains the values that you wish to place in the diagonal of the new matrix.

5. Call each of these functions from the command window on both scalars and vectors. Use Matlab's online help to see what input values are required for each function and what values are returned.

        sin()
        cos()
        tan()
        sqrt()
        log()
        exp()
        isprime()
        length()
        size()
        max()
        min()
        sum()

   Be sure that you can answer these questions.

   What are the units of the input parameters for the trig functions?

   What are the possible return values of the isprime() function?

   What is the value returned by the log() function?