Exercises

Please complete each exercise or answer the question before reviewing the posted solution comments.

Use the clear command before starting your work on a new problem to ensure that any existing variable name assignments don't interfere with your work on the new problem.

1. The decay constant (lambda) of an isotope can be calculated by dividing the natural log of 2 by the half-life (t_1/2). Specifically, the equation is:

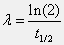
   Iodine-131 is used extensively in nuclear medicine because of its short half-life and useful beta decays. Specifically, the half-life of I-131 is 8.04 days. Use the command line window and Matlab's built-in functions to solve for the decay constant (in [days^-1]).

   0.0862 days^-1 Note: Matlab does not have a built-in ln() function. The built-in function log() function is the natural logarithm.

2. Note: Please complete Question 1 before attempting Question 2. The activity of a radioactive substance is the rate at which decays occur in the sample. Further, the activity can be expressed by the equation:

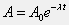
   A radioactive sample has an activity of 4.5 uCi (1 Ci is 3.7E10 disintegrations/second). The half-life of the substance is 68 s. Use Matlab's built-in functions and the command line window to calculate the activity (in uCi) of the substance at t=60 s.

   2.4412 uCi Note: Use the built-in log() function and exp() function in this exercise.