Examples

1. Evaluate 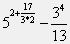using the Command Window in Matlab:

       >> 5^(2+(17/(3*2)))-3^4/13
   
   ans =
   
      2.3835e+003
   
   >> 

   The parentheses are required to override the operator precedence of the power operator ( ^ ). Notice how Matlab uses and displays scientific notation. The result 2.3835e+003 is the value 2.3835x10³. The exponent can be negative as in 3.5e-003 for 3.5x10^-3

2. Use the colon operator to create a vector named multOf3 that contains the multiples of 3 between 3 and 30, inclusive.

   multOf3 = 3 : 3 : 30

3. What is the result of evaluating 3^2^3 in the Command Window?

   The answer is 729 because 3² is 9 and 9³ is 729. If you meant 3⁸, execute 3^(2^3) or 3^8 instead.

4. Body Mass Index (BMI) Example

   Body Mass Index (BMI) is a measurement based on the height and weight of a person. It is calculated by taking a person's weight in kilograms and dividing it by the height (in meters) squared. Body mass index is used in the health care industry as a way to gauge the likelihood of a person developing health problems as a result of having too much body fat. A BMI between 20 and 25 is considered normal and healthy.

   Suppose we wish to determine the body mass indices for a group of people and that the heights and weights of the people are contained in two vectors: the variable height_m contains the heights (in meters) of the people and the variable weight_kg contains the weights of the people, in the same order as was entered in the height_m array. Matlab gives us the capability to perform the same operation on a large amount of data with a few relatively simple commands. Use element-wise operators to calculate the body mass index of each person represented by our data arrays:

       BMI = weight_kg ./ height_m .^ 2

5. Type in the following vector assignment statement and press Enter. What are the initial and final values created?

        a = -3 : 0.5 : 3

       >> a = -3 : 0.5 : 3
   
       a =
   
         Columns 1 through 8 
   
          -3.0000   -2.5000   -2.0000   -1.5000   -1.0000   -0.5000         0    0.5000
   
         Columns 9 through 13 
   
           1.0000    1.5000    2.0000    2.5000    3.0000
   
       >> 

6. Type in the following vector assignment statement and press Enter. What are the initial and final values created? What happens when the range between the initial value and the final value is not evenly divisible by the increment value?

        b = 1 : 3 : 11 

        >> b = 1 : 3 : 11
   
        b =
   
             1     4     7    10
   
        >> 

   If the range is not evenly divisible, then the last value created will be less than the final value in the vector assignment statement.

7. Type in the following vector assignment statement and press Enter. What happens when the final value is less than the initial value?

        e = 10 : 1

       >> e = 10 : 1
   
       e =
   
          Empty matrix: 1-by-0
   
       >>  

   This causes an error because the default increment is positive one and we can never reach 1 by adding positive 1 to the value 10.

8. Type in the following vector assignment statement and press Enter. What happens when the increment is negative?

        c = 10 : -2 : 0 

        >> c = 10 : -2 : 0
   
        c =
   
            10     8     6     4     2     0
   
        >>  

   A negative increment is fine as long as the final value is less than the initial value in the assignment statement.