Exercises

Please complete each exercise or answer the question before reviewing the posted solution comments.

Use the clear command before starting your work on a new problem to ensure that any existing variable name assignments don't interfere with your work on the new problem.

1. Calculate the length of the hypotenuse of the right triangle shown.

   

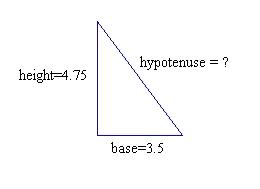
   The length of the hypotenuse is equal to 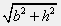, where b is the base and h is the height of the triangle.

   There is no square root operator in Matlab, but there is a built-in function named sqrt. Use this function to calculate the hypontenuse length in the Command Window:

      >> base = 3.5; height = 4.75;
      >> hypontenuse = sqrt(base^2+height^2)
   

   The correct answer is: 5.9002.

   The parenthesis are required and indicate the argument to the sqrt function is the quantity base squared plus height squared. How would the above calculation change if base and height were arrays that contained more than one value?

2. Calculate the temperature of a soda at time t=10 seconds according to the following heat transfer expression where T is the temperature at time t and k is the constant of heat transfer. The initial temperature is 125 degrees and the temperature at time s is 45 degrees. Be sure to assign variables for the information given.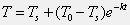

   

   The value of the constant k is 0.45.

   MatLab has a pre-defined function to compute the exponential function named exp. Use this function to solve this problem:

   To solve in Matlab, enter these commands in the Command Window:

      >> T0=125; Ts=45; k=0.45; t=10;
      >> T=(Ts+(T0-Ts)*exp(-k*t))
   

   The correct answer is: 45.8887

3. Use the colon operator to create a vector named squares with the following values:

   1 4 9 16 25 36 49 64 81 100

        squares = 1 : x.^2 : 100

   Hmmm... nice idea! But, this won't work. You can't use an unassigned variable as part of an increment formula. In fact, there's no notation that can solve this directly. There is an iterative algorithm for solving this problem and the following two step process works well.

        n = 1 : 10;
        squares = n .^ 2

   Keep in mind that you often have to solve problems in parts. Be sure to think of ways to break problems in to smaller easier problems as part of your problem solving techniques.

4. Use Matlab to compute the value of this expression.

   

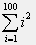
   MatLab has a pre-defined function named sum that you may find useful.

        n = 1 : 100
        n2 = n .^ 2
        result = sum(n2)
        
        result = 
        
          338350