Exercises

Please complete each exercise or answer the question before reviewing the posted solution comments.

1. Write a for loop to display N asterisks (*), one on each line, where N is a number given at the beginning of your script. For example, if N is 5, your script should print out:

   *
   *
   *
   *
   *

   This for loop will display N asterisks on N different lines. Compare this with the while loop that solves the same problem.

   for n = 1 : N
      disp('*');
   end

2. Write a for loop to display N asterisks (*) on one line. Assume that N has already been assigned a number. If N is greater than 80, display only 80 asterisks. If N is less than 1, display no asterisks.

   For example, if N is 5, your script should print out

   *****

   Here is a fragment that will work if N has previously had its value assigned. Notice how the variable starline with N asterisks is created in the loop and it is printed after the loop ends. This is because the disp() command prints a new line after its argument.

   if N > 80
      N = 80;
   end
   starline = '';
   for n = 1 : N
      starline = [starline '*'];
   end
   disp(starline);

   Once again, the for loop is quite convenient syntax for count-controlled loops such as this.

3. Write a code fragment that uses a for loop to repeatedly prompt the user for positive integer or zero. As long as negative values or non-integers are entered, your loop should ask the user for a positive integer.

   Here is a script that will work but has undesireable properties as described following the code.

       val = -1;
       for n = 1 : 100000;
           val = input('Enter a positive integer or zero: ');
           if val >= 0 & rem(val,1) == 0
               break;    % break out of the loop when a valid value is found
           end
       end

   The use of break statements is generally discouraged due to the increased difficulty in following the control flow of programs that use break statements. Such loops have two (or more) ways to exit or stop the loop, this makes them harder to debug than loops that have only one exit point.

   Also, the use of the value 100000 or other similarily large value is logically incorrect and this also makes the code harder to maintain. We really don't want this loop to execute a large number or infinite number of times only until the user enters a valid value. Iteration that should repeat until a condition is met (or while a bad condition exists) should be implemented with a while loop as shown here:

       val = -1;
       while val < 0 | rem(val,1) ~= 0
           val = input('Enter a positive integer or zero: ');
       end

4. Write a for loop that counts the number of values in a vector that are equal to some number N and displays that value in a user-friendly way. (Hint: Use disp to include text and values.) Assume that the vector is saved as values and that N has already been assigned.

   This fragment assumes that N and values have already been assigned. This could be the case if the fragment was in the body of a function or nested inside of some other code fragment.

   K = length(values);   % index of last value to check
   count = 0;            % initialize a counter variable
   
   for k = 1 : K
      if values(k) == N
          count = count + 1;
      end
   end
   
   disp(['There are ', num2str(count), ' values of ', num2str(N),' in the vector ']);
   

5. Write a script that uses a for loop to compute and plot the finite Fourier series given by the sum: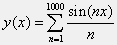

   

   over the interval x=(0,8 ). The plot you should see is called the 'sawtooth function'.

   Here's one algorithm (set of steps) for solving this problem with iteration (loops):

   1. Create a vector with many x values in the range (to plot a continuous curve).
   2. Create a vector of y values with the initial value of 0 that correspond to the x vector created.
   3. For each value n from 1 to 1000
      1. Replace each value in y with the calculated value y + sin(n*x)/n.
   4. Plot x vs y and label the axis.

   % one way to plot the sawtooth using a for loop
   clear;
   x=[0:0.1:8] * pi;  % range from 0 to 8pi with last entry actually 8pi
   
   y = 0*x;           % total starts at 0 for each value of x
                      % creates a vector with the same number of values as in x,
                      % but each value is 0
   
   % Compute the fournier series for each value of x
   for n = 1:1000
       y = y + sin(n*x)/n;  % do not need element-wise operators here
   end                      % because n is a scalar (inside the loop)
   
   plot(x,y);
   axis([x(1) x(length(x)),  -pi/2, pi/2])
   title('first method')
   

6. Write a script that implements this algorithm to plot the finite Fourier series given above:

   1. Create a vector of the n values from 1 to 1000.
   2. Initialize an index variable i to 1. This value indicates which index in y to store the calculate value.
   3. For each value x from 1 to 8
      1. Calculate the value sum(sin(n*x)./n) to put the sum of all sin(n*x)./n values and store the sum in position i of y
      2. Increment the index i value for the next iteration.
   4. Plot x vs y and label the axis.

   % a second iterative way to plot the sawtooth function
   clear; figure;
   n = 1:1000;
      
   i=1; % initialize the index to the first index of y
   for x = [0:0.1:8] * pi
   
       y(i) = sum(sin(n*x)./n);    % need element-wise division, n is a vector here
                                   % save value in position i of y
   
       i = i + 1;                  % update the index for the next iteration
   
   end
   
   x = [0:0.1:8] * pi
   plot(x,y);
   axis([x(1) x(length(x)),  -pi/2, pi/2])
   title('second method')