for Loop

The structure of a for loop:

for counter = first : increment : last
    statements  % body of for loop
end

The form of a for loop is interpreted as follows:

The variable counter is often called the counter variable. This variable will take on each successive value of the vector created in the first line of the loop. The current value of counter can be used inside of the body of the for loop. Any valid variable name can be used for the counter variable. Common choices are: n, k, and j.

The code first:increment:last is like the vectors we have created using the colon (:) operator in earlier lessons.

Even though the for loop condition has a different form than that found in the while loop, it is still evaluated as a boolean expression. The condition of the for loop compares the current value of the counter variable, n, with the value of last. If the value of the counter variable is less than or equal to the value in last, the body of the loop will execute.

The control flow diagram of a for loop looks like:

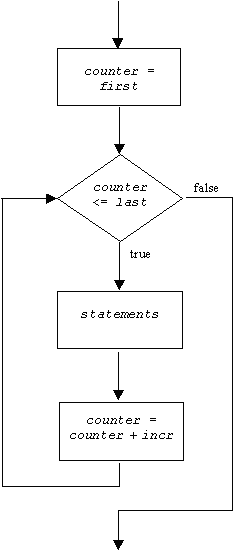
The for loop is equivalent to the following while loop:

counter = first;
while counter <= last
    statements  % body of the loop
    counter = counter + incr;
end

We can leave out the increment part of the condition. If we leave it out, Matlab uses an increment of 1. In other words, first : last is equivalent to first : 1 : last (just as it was when we used the colon operator to create and manipulate matrices). We can rewrite our program to sum the odd integers from 1 to 1,000,001 so it uses a for loop in the following way:

sum = 0;
last = 10^6 + 1;   % 1,000,001
for num = 1 : 2 : last
    sum = sum + num;
end
disp(sum)

This results in code that is more compact (but still readable). The for statement is useful for constructing the matrices required to solve complex linear systems. The index (or counter) of the for statement can be used as the index of a vector or matrix. In the following code fragment, we first create a 10 x 10 matrix of zeros and then put the numbers 0 to 9 along the diagonal:

zmat = zeros(10, 10);
for k = 1 : 10
    zmat(k, k) = k-1;
end
disp(zmat)

This code works as follows:

1. Create the matrix zmat, with ten columns and ten rows, containing all zeros.
2. Set k to 1.
3. If k is less than or equal 10, execute the body.
   1. assign the value k-1 to the element at position k,k in the matrix zmat.
   2. Increment the value of k by the increment amount (1 in this example).
   3. Repeat this step.
4. Else, continue to the next step.
5. Display the values in zmat.

It is sometimes better to use a more general form when specifying the range of values to iterate over in the first line of a for loop. For example, in place of the 10 in the first line of the loop in the previous example, we could have used length(zmat). Recall that, for a matrix, the length function returns the larger of the number of rows and number of columns (since zmat is a square matrix, the number of rows is the same as the number of columns). By doing this, we make it easier to modify our program to handle square matrices of other sizes, for example, we can now put the values 0 to 19 along the diagonal of a 20 x 20 matrix just by changing the values in the zeros function:

zmat = zeros(20, 20);
for k = 1 : length(zmat)
    zmat(k, k) = k-1;
end
disp(zmat)

We can make our program even more general (and easier to modify to handle square matrices of other sizes) by using a variable to hold the number of elements in a row (or column):

N = 20;              % N = # of rows (also # of columns)
zmat = zeros(N, N);  % so zmat is a N x N matrix
for k = 1 : N
    zmat(k, k) = k-1;
end
disp(zmat)

Using variables instead of numbers in our code is what makes programming solutions to problems better than simply solving the individual problem. A general solution can be used for an entire classes of problems. Once we write and debug the code for a type of problem instead of just a specific instance of a problem, we can execute our code for any new instances of that type of problem.