Examples
Find the area under the curve
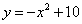
Define this function to make the solution easier to read and debug.
function y = f01( x ) y = -x.^2 + 10;
Then write a script that finds the roots and calculates the area under the curve from one root to another.
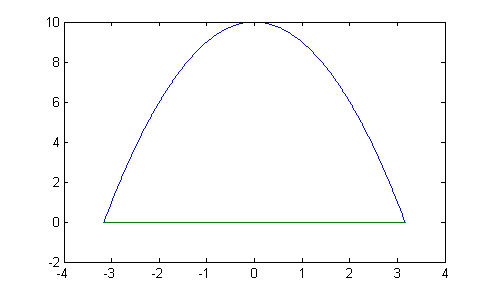
% Calculate the area under the curve % y = -x^2+10 % First, find the roots using our user-defined function x1 = fzero('f01', -2) x2 = fzero('f01', 2) % Next, find the area between the roots x1 and x2 area = quad( 'f01', x1, x2 ) % Finally, plot area in question results xx = [x1:0.01:x2]; yy = f01(xx); plot(xx,yy, [x1 x2], [0 0]);The results are:
x1 = -3.16227766016838 x2 = 3.16227766016838 area = 42.16370213557839
If the limits of integration are not given and you are asked to find the area under a curve, you will first need to find the roots of the function. Use
fzeroto find the roots in Matlab.What is the result of calculating the area of the above curve with a range that is larger than from one root to another?
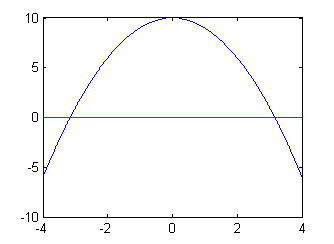
% Find the area under the curve in Example 1 between -4 and 4 area2 = quad( 'f01', -4, 4 )
The results are:
>> quad( 'f01', -4, 4 ) area2 = 37.33333333333333
The area found here is less than that found in Example 1 because the area that is "under" the x-axis and above the curve is subtracted from the previous calculated area. This is usually an error. Be sure that you understand how the value of the curve is being used in the integral that calculates the area.
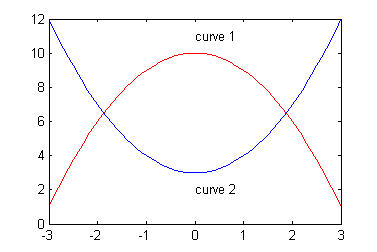
Find the area between these two curves:
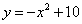 and
and 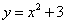
- Define a function that calculates the difference between the two functions.
function y_diff = f1_minus_f2( x ) f1 = -x.^2 + 10; f2 = x.^2 + 3; y_diff = f1 - f2;
- Find where your new function equals zero (find roots).
x1 = fzero('f1_minus_f2', -1); x2 = fzero('f1_minus_f2', 3); - Find the area of your new function between the two intersection points.
area_btw_f1_f2 = quad('f1_minus_f2',x1,x2)
The work to define a new function is a small effort compared to the work it saves you in performing the other required operations. The final code is much more readable also.
Just be sure to test your function to determine that it returns the value that you are interested in. For example
f1_minus_f2(0)should return7because this is the positive difference between the y-intercepts of the two curves. If the result is negative then your function is incorrectly subtracting value of the larger function from the value of the smaller function. This should be noticed and fixed before using your function to calculate the area between the two curves.- Define a function that calculates the difference between the two functions.

