Exercises
Please complete each exercise or answer the question before reviewing the posted solution comments.
-
You are working with a tank that has a radius that varies by height according to the following relationship (all measurements in feet):
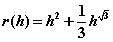
We can find the volume of a container with varying radius by using the following expression:
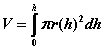
Therefore, the integral we need to evaluate to find the volume of a tank that is H feet high and a radius that is a function of height according to r(h) above, is:
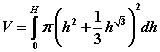
Use Matlab to determine the volume (evaluate the integral) for such a tank that is 5 feet high:
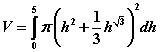
First, define a function that returns the cross-sectional area of the tank at a specified height.
function xarea = tank_cross_section(h) % Returns the cross-sectional area of a tank xarea = pi*(h.^2+(1/3)*h.^sqrt(3)).^2;Notice the periods, this is so that the function still will work when a matrix is passed to it. This allows the
quadfunction to have the function evaluate more than one value at a time. This ability is required forquadto correctly determine the result.Compute the value by typing:
>> quad('tank_cross_section',0,5)Matlab will return with
ans = 2.9652e+003In other words, our tank volume is 2965.2 cubic feet. Remember, if you plan to use this value again, name it (such asTVol = quad('tank',0,5). That way,TVol = 2965.2)Note: Although it is good programming practice to define the function in a separate M-file, the
quadfunction can be executed with the single line:>> TVol = quad('pi*(h.^2+(1/3)*h.^sqrt(3)).^2',0,5)

