Examples:
- Type these commands in a Maple worksheet and pay careful attention to the results of each entering each keystroke in the Maple worksheet.
eq1 := x^2 -> - 5*x + 6 = 0 s1 := solve(eq1,x)
- Type these commands in a Maple worksheet and pay careful attention to the results of each entering each keystroke.
eq2 := x^3 -> - 9*x^2 -> + 26*x - 24 = 0 s2 := solve( eq2, x )
- Type these commands in a Maple worksheet and pay careful attention to the results of entering each keystroke and typing the [Enter] key.
eq7 := x^2 -> - 17/6 -> *x - 7/3 -> = 0 s7 := solve(eq7, x) s7_1 s7_2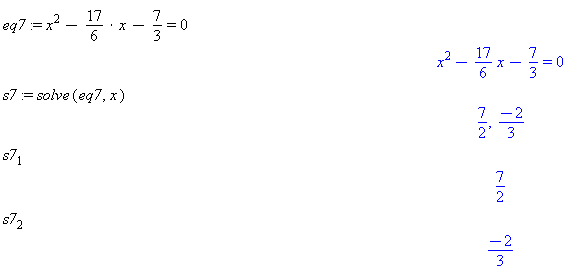
Comment: Note the underscore
_character is used to to create or access subscripted variables. Subscript 1 accesses the first solutions and so on. The square brackets[ ]can be used to do the same.Try
s7[1]ands7[2]to compare the results. We commend using the[ ]notation to avoid some subtle issues that arise when using the subscript or underscore notation. eq8 := x^4 -> -313/315 -> * x^3 -> + 1/189 -> * x^2 -> + 179/945 -> * x - 2/63 -> = 0 solve(eq8,x)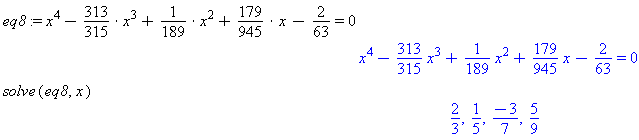
Comment: Note how Maple can find the roots of very complex polynomials if the roots are rational fractions.
eq9: = a*x^3 -> + b*x^2 -> + c*x + d = 0 solve(eq9, x)
Comment: In this case Maple gives you the formula for the solution of a cubic equation in terms of the coefficients a, b, c, and d.
eq10 := x^(3/2)*ln(x) - 7 = 0 solve(eq10, x) fsolve(eq10, x)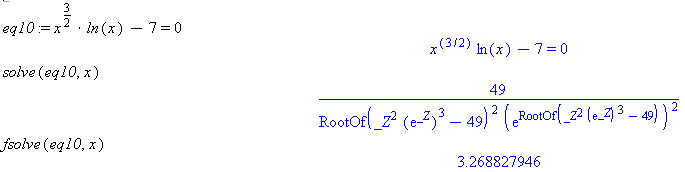
Comment: The numerical answer is returned as a decimal result because a successive approximation numerical method was used to find the solution. This would be difficult to do with paper and pencil because the computer was required to execute many iterations to get this result to such high accuracy. You should always attempt to solve equations using the Solve option or the
solvecommand. If this does not work, then use theSolve numericallyor thefsolvecommand.

