Solving for the roots of one algebraic equation and one unknown
Finding the roots of a single linear algebraic equation with one unknown variable is of course trivial.
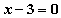 has the solution x=3 and we know there is just a single root.
This is middle school algebra where the concept of an unknown variable is introduced.
has the solution x=3 and we know there is just a single root.
This is middle school algebra where the concept of an unknown variable is introduced.
Finding the roots of a quadratic algebraic equation with one unknown variable is also familiar to everyone because the equations can be factored by inspection and a formula for the roots exists and we know there are two roots.
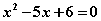 can be factored as
can be factored as
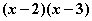 and has the roots
and has the roots
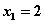 and
and
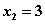 .
.
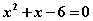 can be factored as
can be factored as
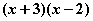 and has the roots
and has the roots
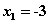 and
and
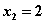 .
.
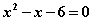 can be factored as
can be factored as
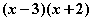 and has the roots
and has the roots
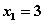 and
and
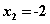 .
.
You can solve for the roots of algebraic equations by typing the solve command into the Maple document and Maple will return the roots.
eq1 := x^2 → - x - 6 = 0
solve( eq1, x )
Alternatively, you can enter the equation to be solved into
the Maple document and then right-click on the equation and select
the Solve option.
In either case, Maple returns the two solutions using the rules of
algebra. The solutions are returned in symbolic form, not decimal form.
You can also solve for the roots using a numerical successive approximation method called Newton's Method, named after Isaac Newton, who invented it. [Newton's Method will be discussed in another module in more detail]. To use this numerical method, enter the command
fsolve( eq1, x, x=0..6 )
Do not mistake the similarity of the solve and
fsolve confuse you. They both can be used to solve an
equation, but fsolve finds an approximate value for
one of the solution values using a numeric technique. It is not
an exact solution and it will not necessarily find the solution you seek unless you specify
the correct range for the solution. It can sometimes find multiple solutions,
but typically returns only a single solution.
You should always try to symbolically solve the equation first. Only if Maple cannot find a symbolic solution, should you be satisfied with the numerical approximation.

