Examples:

1. Consider this simple ODE that can be solved symbolically.

             y'=2t, y(0)=1
           

   The solution is

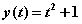
   We can find the symbolic solution in two ways, by hand with integration methods and with Maple.

   By hand solution

   
   integrate both sides
   
   
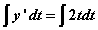
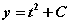
   use the initial condition to find C
   

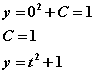
   Symbolic ODE Solution in Maple

   1. Enter the ode.
   2. Use dsolve to solve the ODE.

   As shown here, the result is a symbolic expression for the function y(t).

   

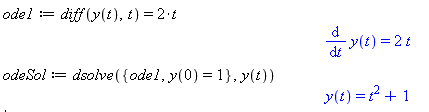
2. Or, we can find a numeric solution by using Euler's Method.

   Euler's Method

   Choose h=0.2 and solve from 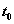to .

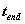   k	0	1	2	3	4	5	6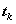
   	0	0.2	0.4	0.6	0.8	1.0	1.2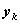
   	1	1	1.08	1.24	1.48	1.80	2.20

   In the figure below the approximate (numeric) solution produced by Euler's method is compared to the exact solution.

   

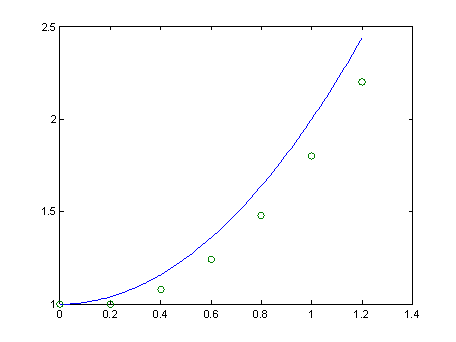
   Notice that the numerical solution (circles) deviates substantially from the exact solution (blue curve). We can improve the accuracy of the numerical solution by reducing the value of the time step h. By doing so, the finite difference more accurately approximates the actual derivative

3. Yet another way, is to solve ODE's numerically in Maple by using the numeric option in the dsolve command.

   Numeric ODE Solution to y'=2t in Maple

   1. Enter the ode.
   2. Substitute values for any constants. There are none in this example.
   3. Use dsolve command to get a numeric result (proc). Note: The result is not a symbolic formula, but rather a procedure. This procedure can be used to get one result, or many.
   4. Use the odeNumSol proc result to find the numeric approximation of y(1.2). Notice how accurate the approximation generated by dsolve.
   5. Use the proc to plot the solution from t=0 to t=2:

   

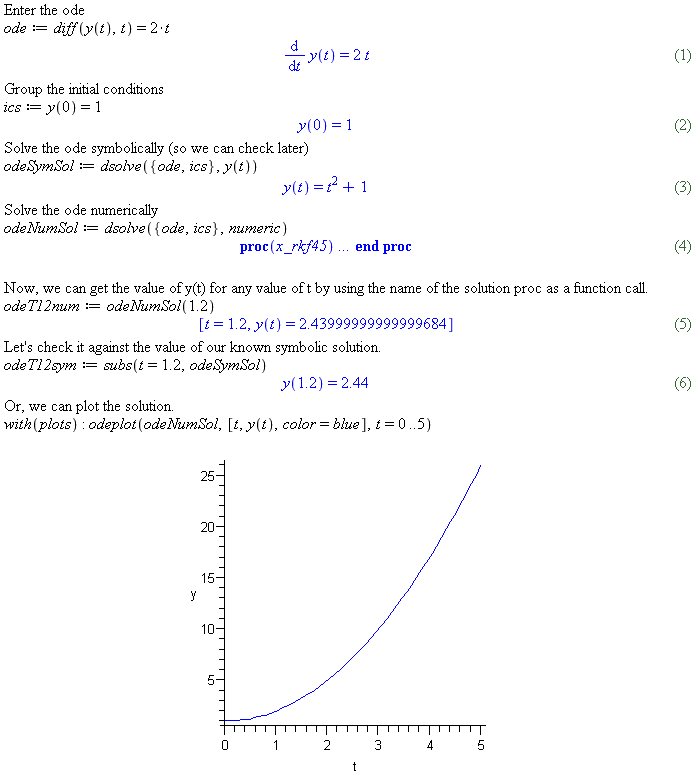
   By default, the dsolve command uses Fehlberg fourth-fifth order Runge-Kutta method. You will learn about Runge-Kutta Methods in the next lessons. The Runge-Kutta methods are much more accurate than Euler's. Other numeric methods can be specified to dsolve, but that use of the dsolve command is not covered in our course.

   The next lessons will show you how these more accurate numeric methods work. You will quickly notice that they are more complex and time consuming to produce.

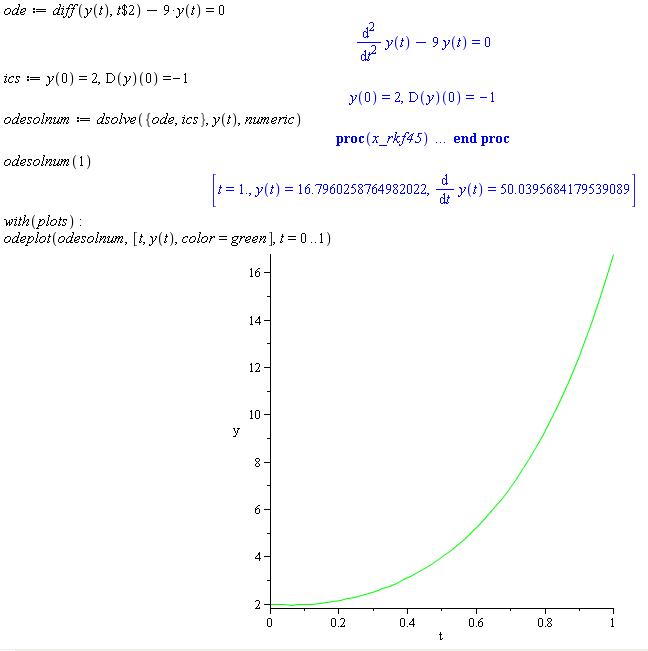
4. Use Maple to plot a numeric solution to this second order ODE:
   
   y" - 9y = 0 when y(0)=2 and y'(0)=-1

   1. Enter the ode.
   2. Enter the initial conditions.
   3. Substitute values for any constants in both the odes and the initial conditions. (none in this case)
   4. Use dsolve command with the numeric optoin to get a numeric result (proc). Note: The result is not a symbolic formula, but rather a procedure. This procedure can be used to get one result, or many.
   5. Test the numeric solution proc result to find the numeric approximation of y(1). Notice how accurate the approximation generated by dsolve.
   6. Plot the solution proc from t=0 to t=10.

   

   Special Notes regarding numeric solutions to Second Order ODEs:

   The initial conditions must be included to numerically solve an ode system. Pay special attention to the syntax for entering the initial condition of the second derivative. You must use this syntax, D(y)(0)=-1, to enter the y'(0)=-1 initial condition. If you have two second order ODEs, you will need two initial conditions for each ODE, for a total of four initial conditions. Also, you must first sustitute values for any symbolic constants in the ODE or initial conditions.

5. Use Maple to symbolically solve and then plot the symbolic solution for the same second order ODE. Compare the results at t=1.
   
   The ODE and initial conditions are:
   
   y" - 9y = 0 when y(0)=2 and y'(0)=-1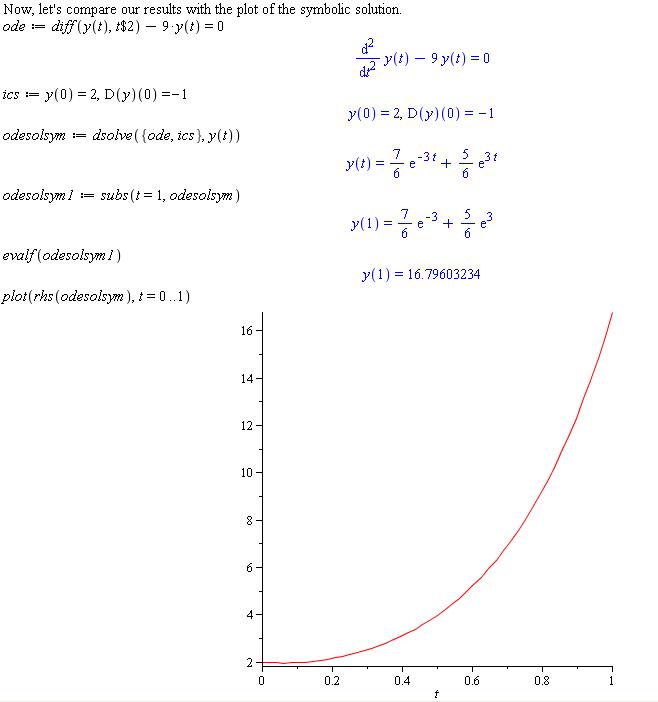

   

   Note: The initial conditions must be included to get a solution that can be plotted. Also, you would need to sustitute values for any symbolic constants in the solution before plotting.