Prev: W1, Next: W3
Links: Zoom, TopHat (010339, or Form), Calculator:
Slide:
# Red Black Trees
📗 Red Black Trees (RBT) are Binary Search Trees (BST) that stay balanced (self balancing).
➩ Each node is either red or black. (null children are considered black.)
➩ The root node is black.
➩ No red nodes have red children.
➩ Every path from root to a null child has the same number of black nodes (black height of the tree).
📗 Visualization: Link.
# RBT Example
ID:📗 [1 point] Recolor the BST so that it is a RBT.
# RBT Balance
📗 Compare the longest and shortest paths:
➩ Identical black lengths \(H_{b}\).
➩ Shortest paths have \(H_{b} = O\left(\log\left(N\right)\right)\) lengths.
➩ Longest paths have \(2 H_{b} = O\left(2 \log\left(N\right)\right) = O\left(\log\left(N\right)\right)\) lengths.
➩ \(H = O\left(\log\left(N\right)\right)\) for RBTs.
# Inserting into a RBT
📗 Insert new value using BST insertion algorithm.
📗 Color the new node red.
📗 Check RBT properties and restore if necessary.
➩ The root node is black.
➩ No red nodes have red children.
# Repair RBT after Insert
📗 Repair a red root:
➩ If the root of the tree is red, switch it to black without violating any other property.
📗 Repair red node with red child:
➩ If parent's sibling (aunt) is black or null: (rotate) then rotate and color swap.
➩ If parent's sibling is red: recolor then check.
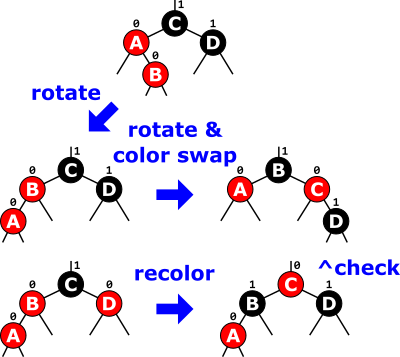
# RBT Insert Example
ID:📗 [1 point] Insert the following nodes: (click the "Insert" square to insert this node to the BST).
➩ Rotate the tree from A to B by dragging A to B in the diagram.
📗 List of nodes:
# RBT Insert Another Example
📗 Another example from Campus section: 7, 14, 18, 23, 1, 11, 20, 29, 25, 27
# Deleting from a RBT
📗 Delete value using the BST deletion algorithm.
📗 Check RBT properties and restore if necessary.
# Repair RBT after Delete
📗 If deleted node is black and replacement is red, turn replacement black.
📗 Otherwise:
➩ rotate and color swap then rotate and color swap and recolor.
➩ recolor then check.
➩ rotate and color swap then check.
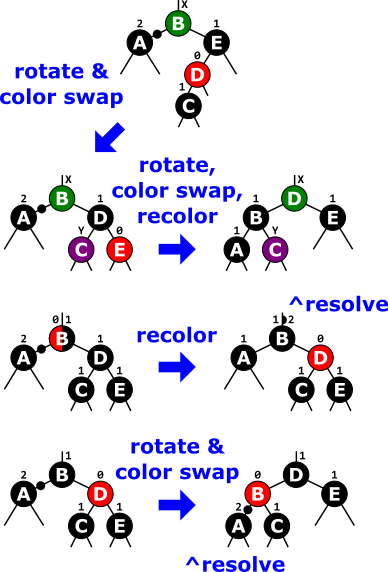
# RBT Delete Example
ID:📗 [1 point] Delete the following nodes: (click the "Delete" square to delete this node from the BST).
➩ Rotate the tree from A to B by dragging A to B in the diagram and mark a node as a double by dragging the node to anywhere else.
📗 List of nodes:
📗 Use left child to replace:
# RBT Delete Same Example
📗 Drawing null nodes might be easier in some cases.
ID: 📗 [1 point] Delete the following nodes: (click the "Delete" square to delete this node from the BST).
➩ Rotate the tree from A to B by dragging A to B in the diagram and mark a node as a double by dragging the node to anywhere else.
📗 List of nodes:
📗 Use left child to replace:
# RBT Delete Another Example
📗 Another example from Campus section: 14, 7, 5, 1, 6, 11, 9, 13, 20, 18, 15, 19, 23, 29 (RED: 5, 11, 15, 19, 29)
📗 Delete: 15, 23, 20, 13, 29, 1, 5, 6
# Complexity of RBT Operations
📗 Search: \(O\left(H\right) = O\left(\log\left(N\right)\right)\)
📗 Insert: \(O\left(H\right) = O\left(\log\left(N\right)\right)\)
📗 Delete: \(O\left(H\right) = O\left(\log\left(N\right)\right)\)
# Testing
📗 3 dimensions for tests:
➩ Unit test ----- Integration test
➩ Opaque-box test ----- Clear-box test
➩ Input-output test ----- Property test
# Readings
📗 Notes from the Campus section: Link
📗 JAR file guide: Link
📗 JUnit assertions class: Link
📗 JUnit user guide: Link
test rbt,rin,rde,rdn l
📗 Notes and code adapted from the course taught by Professor Florian Heimerl and Ashley Samuelson.
📗 Please use Ctrl+F5 or Shift+F5 or Shift+Command+R or Incognito mode or Private Browsing to refresh the cached JavaScript.
📗 You can expand all the examples and demos: , or print the notes: .
📗 If there is an issue with TopHat during the lectures, please submit your answers on paper (include your Wisc ID and answers) or this Google Form at the end of the lecture.
Prev: W1, Next: W3
Last Updated: December 29, 2025 at 9:44 PM