Prev: L12, Next: L14
Course Links: Canvas, Piazza, TopHat (212925)
Zoom Links: MW 4:00, TR 1:00, TR 2:30.
Tools
📗 You can expand all TopHat Quizzes and Discussions: , and print the notes: , or download all text areas as text file: .
📗 For visibility, you can resize all diagrams on page to have a maximum height that is percent of the screen height: .
📗 Calculator:
📗 Canvas:
pen
# Midterm Information
📗 See Canvas announcement and Link.
TopHat Game
📗 We will post questions that are very similar to the questions on the exam based on your choices in this TopHat coordination game.
➩ A: We will post 1 question if more than 75 percent of you choose A.
➩ B: We will post 2 questions if more than 90 percent of you choose B.
➩ C: We will post 0 questions.
➩ D: We will post 0 questions.
➩ E: We will post 0 questions.
# Natural Language Processing Tasks
📗 Supervised learning:
➩ Speech recognition.
➩ Text to speech.
➩ Machine translation.
➩ Image captioning (combines with convolutional networks).
📗 Other similar sequential control or prediction problems:
➩ Handwritting recognition (online recognition: input is a sequence of pen positions, not an image).
➩ Time series prediction (for example, stock price prediction).
➩ Robot control (and other dynamic control tasks).
# Recurrent Networks
📗 Dynamic system uses the idea behind bigram models, and uses the same transition function over time:
➩ \(a_{t+1} = f_{a}\left(a_{t}, x_{t+1}\right)\) and \(y_{t+1} = f_{o}\left(a_{t+1}\right)\)
➩ \(a_{t+2} = f_{a}\left(a_{t+1}, x_{t+2}\right)\) and \(y_{t+2} = f_{o}\left(a_{t+2}\right)\)
➩ \(a_{t+3} = f_{a}\left(a_{t+2}, x_{t+3}\right)\) and \(y_{t+3} = f_{o}\left(a_{t+3}\right)\)
➩ ...
📗 Given input \(x_{i,t,j}\) for item \(i = 1, 2, ..., n\), time \(t = 1, 2, ..., t_{i}\), and feature \(j = 1, 2, ..., m\), the activations can be written as \(a_{t+1} = g\left(w^{\left(a\right)} \cdot a_{t} + w^{\left(x\right)} \cdot x_{t} + b^{\left(a\right)}\right)\).
➩ Each item can be a sequence with different number of elements \(t_{i}\), therefore, each item has different number of activation units \(a_{i,t}\), \(t = 1, 2, ..., t_{i}\).
➩ There can be either one output unit at the end of each item \(o = g\left(w^{\left(o\right)} \cdot a_{t_{i}} + b^{\left(o\right)}\right)\), or \(t_{i}\) output units one for each activation unit \(o_{t} = g\left(w^{\left(o\right)} \cdot a_{t} + b^{\left(o\right)}\right)\).
📗 Multiple recurrent layers can be added where the previous layer activation \(a^{\left(l-1\right)}_{t}\) can be used in place of \(x_{t}\) as the input of the next layer \(a^{\left(l\right)}_{t}\), meaning \(a^{\left(l\right)}_{t+1} = g\left(w^{\left(l\right)} \cdot a^{\left(l\right)}_{t} + w^{\left(l-1\right)} \cdot a^{\left(l-1\right)}_{t+1} + b^{\left(l\right)}\right)\).
📗 Neural networks containing recurrent units are called recurrent neural networks: Wikipedia.
➩ Convolutional layers share weights over different regions of an image.
➩ Recurrent layers share weights over different times (positions in a sequence).
TopHat Discussion
📗 [1 points] Which weights (including copies of the same weight) are used in one backpropogation through time gradient descent step when computing \(\dfrac{\partial C}{\partial w^{\left(x\right)}}\)? Use the slider to unfold the network given an input sequence.
Input sequence length: 1
Output is also a sequence:
1 slider
# Backpropogation Through Time
📗 The gradient descent algorithm for recurrent networks are called Backpropagation Through Time (BPTT): Wikipedia.
📗 It computes the gradient by unfolding a recurrent neural network in time.
➩ In the case with one output unit at the end, \(\dfrac{\partial C_{i}}{\partial w^{\left(o\right)}} = \dfrac{\partial C_{i}}{\partial o_{i}} \dfrac{\partial o_{i}}{\partial w^{\left(o\right)}}\), and \(\dfrac{\partial C_{i}}{\partial w^{\left(a\right)}} = \dfrac{\partial C_{i}}{\partial o_{i}} \dfrac{\partial o_{i}}{\partial a_{t_{i}}} \dfrac{\partial a_{t_{i}}}{\partial w^{\left(a\right)}} + \dfrac{\partial C_{i}}{\partial o_{i}} \dfrac{\partial o_{i}}{\partial a_{t_{i}}} \dfrac{\partial a_{t_{i}}}{\partial a_{t_{i} - 1}} \dfrac{\partial a_{t_{i} - 1}}{\partial w^{\left(a\right)}} + ... + \dfrac{\partial C_{i}}{\partial o_{i}} \dfrac{\partial o_{i}}{\partial a_{t_{i}}} \dfrac{\partial a_{t_{i}}}{\partial a_{t_{i} - 1}} ... \dfrac{\partial a_{2}}{\partial a_{1}} \dfrac{\partial a_{1}}{\partial w^{\left(a\right)}}\), and \(\dfrac{\partial C_{i}}{\partial w^{\left(x\right)}} = \dfrac{\partial C_{i}}{\partial o_{i}} \dfrac{\partial o_{i}}{\partial a_{t_{i}}} \dfrac{\partial a_{t_{i}}}{\partial w^{\left(x\right)}} + \dfrac{\partial C_{i}}{\partial o_{i}} \dfrac{\partial o_{i}}{\partial a_{t_{i}}} \dfrac{\partial a_{t_{i}}}{\partial a_{t_{i} - 1}} \dfrac{\partial a_{t_{i} - 1}}{\partial w^{\left(x\right)}} + ... + \dfrac{\partial C_{i}}{\partial o_{i}} \dfrac{\partial o_{i}}{\partial a_{t_{i}}} \dfrac{\partial a_{t_{i}}}{\partial a_{t_{i} - 1}} ... \dfrac{\partial a_{2}}{\partial a_{1}} \dfrac{\partial a_{1}}{\partial w^{\left(x\right)}}\).
➩ The case with one output unit for each activation unit is similar.
TopHat Discussion
📗 [1 points] Which weights (including copies of the same weight) are used in one backpropogation through time gradient descent step when computing \(\dfrac{\partial C}{\partial w^{\left(x\right)}}\)? Use the slider to unfold the network given an input sequence.
Input sequence length: 1
Output is also a sequence:
1 slider
# Vanishing and Exploding Gradient
📗 Vanishing gradient: if the weights are small, the gradient through many layers will shrink exponentially to \(0\).
📗 Exploding gradient: if the weights are large, the gradient through many layers will grow exponentially to \(\pm \infty\).
📗 In recurrent neural networks, if the sequences are long, the gradients can easily vanish or explode.
📗 In deep fully connected or convolutional networks, vanishing or exploding gradient is also a problem.
# Gated Recurrent Unit and Long Short Term Memory
📗 Gated hidden units can be added to keep track of memories: Link.
➩ Technically adding small weights will not lead to vanishing gradient like multiplying small weights, so hidden units can be added together.
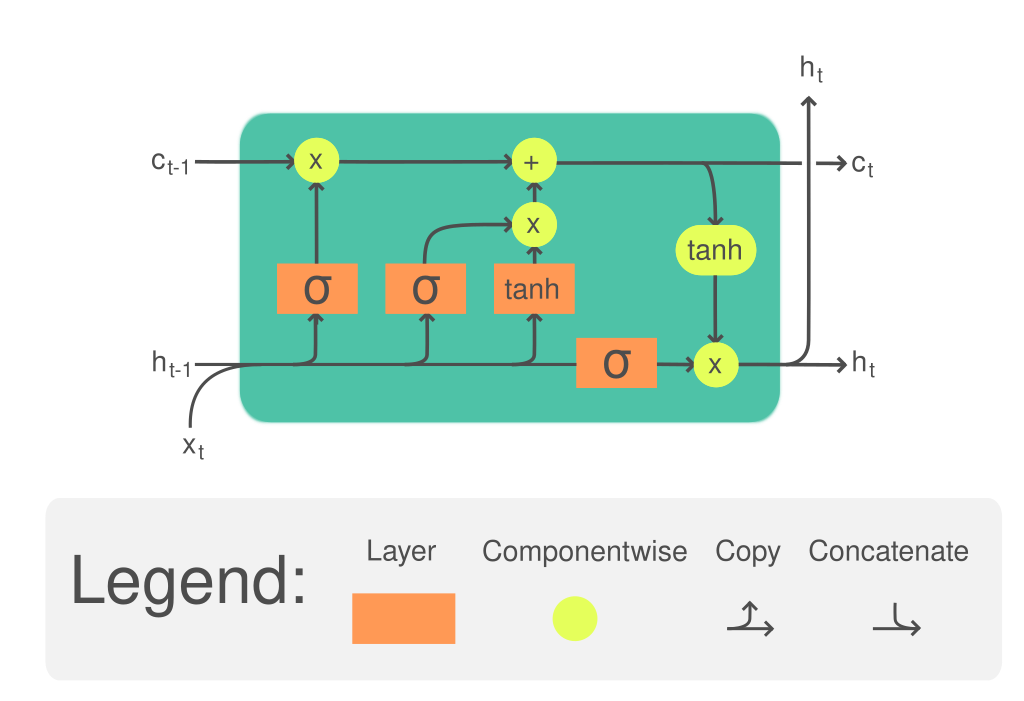
📗 Long Short Term Memory (LSTM): Wikipedia.
➩ The (long term) memory is updated by \(a^{\left(c\right)}_{t} = a^{\left(f\right)}_{t} \times a^{\left(c\right)}_{t-1} + a^{\left(i\right)}_{t} \times a^{\left(g\right)}_{t}\), where \(a^{\left(c\right)}\) is called the cell unit, \(a^{\left(f\right)}\) is the forget gate and controls how much memory to forget, \(a^{\left(i\right)}\) is the input gate and controls how much information to add to memory, \(a^{\left(g\right)}\) is the new values added to memory.
➩ The (short term memory) state is updated by \(a^{\left(h\right)} = a^{\left(o\right)} \times g\left(a^{\left(c\right)}_{t}\right)\), where \(a^{\left(h\right)}\) is the usual recurrent unit called hidden state, \(a^{\left(o\right)}\) is the output gate and controls how much information from the memory to reflect in the next state.
➩ Each of the gates are computed based on the hidden state and the input features (or the previous layer hidden states if there are multiple LSTM layers): \(a^{\left(f\right)}_{t} = g\left(w^{\left(f\right)} \cdot x_{t} + w^{\left(F\right)} \cdot a^{\left(h\right)}_{t-1} + b^{\left(f\right)}\right)\), \(a^{\left(i\right)}_{t} = g\left(w^{\left(i\right)} \cdot x_{t} + w^{\left(I\right)} \cdot a^{\left(h\right)}_{t-1} + b^{\left(i\right)}\right)\), \(a^{\left(g\right)}_{t} = g\left(w^{\left(g\right)} \cdot x_{t} + w^{\left(G\right)} \cdot a^{\left(h\right)}_{t-1} + b^{\left(g\right)}\right)\), \(a^{\left(o\right)}_{t} = g\left(w^{\left(o\right)} \cdot x_{t} + w^{\left(O\right)} \cdot a^{\left(h\right)}_{t-1} + b^{\left(o\right)}\right)\).
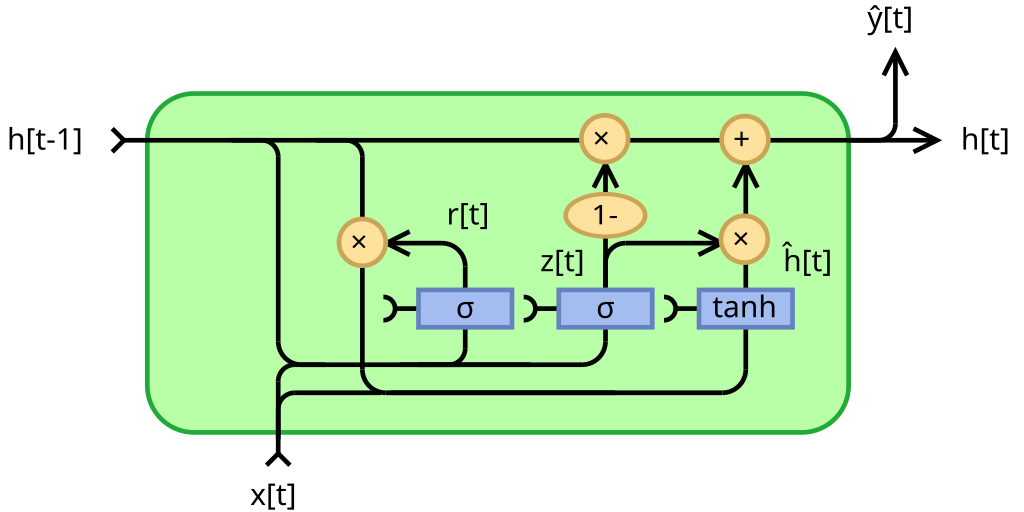
📗 Gated Recurrent Unit (GRU): Wikipedia.
➩ The memory is also updated through addition: \(a^{\left(h\right)}_{t} = \left(1 - a^{\left(z\right)}_{t}\right) \times a^{\left(h\right)}_{t-1} + a^{\left(z\right)}_{t} \times a^{\left(g\right)}_{t}\), where \(a^{\left(z\right)}\) is the update gate, and \(a^{\left(r\right)}\) is the reset gate.
➩ Each of the gates are computed in a similar way: \(a^{\left(z\right)}_{t} = g\left(w^{\left(z\right)} \cdot x_{t} + w^{\left(Z\right)} \cdot a^{\left(h\right)}_{t-1} + b^{\left(z\right)}\right)\), \(a^{\left(r\right)}_{t} = g\left(w^{\left(r\right)} \cdot x_{t} + w^{\left(R\right)} \cdot a^{\left(h\right)}_{t-1} + b^{\left(r\right)}\right)\), \(a^{\left(g\right)}_{t} = g\left(w^{\left(g\right)} \cdot x_{t} + w^{\left(G\right)} \cdot a^{\left(r\right)}_{t} \times a^{\left(h\right)}_{t-1} + b^{\left(g\right)}\right)\).
Example
📗 GRU:
📗 LTSM:
test rnn,bpt q
📗 Notes and code adapted from the course taught by Professors Jerry Zhu, Yingyu Liang, and Charles Dyer.
📗 Content from note blocks marked "optional" and content from Wikipedia and other demo links are helpful for understanding the materials, but will not be explicitly tested on the exams.
📗 Please use Ctrl+F5 or Shift+F5 or Shift+Command+R or Incognito mode or Private Browsing to refresh the cached JavaScript.
📗 You can expand all TopHat Quizzes and Discussions: , and print the notes: , or download all text areas as text file: .
📗 If there is an issue with TopHat during the lectures, please submit your answers on paper (include your Wisc ID and answers) or this Google form Link at the end of the lecture.
📗 Anonymous feedback can be submitted to: Form.
Prev: L12, Next: L14
Last Updated: January 19, 2026 at 9:18 PM