Prev: M4 Next: M6
Back to week 2 page: Link
# M5 Written (Math) Problems
📗 Enter your ID (the wisc email ID without @wisc.edu) here: and click (or hit the "Enter" key) 1,2,3,4,5,6,7,8,9,10,11 m5
📗 You can also load from your saved file
and click .
and click .
📗 If the questions are not generated correctly, try refresh the page using the button at the top left corner.
📗 The official deadline is July 3, late submissions within a week will be accepted without penalty, but please submit a regrade request form: Link.
📗 The same ID should generate the same set of questions. Your answers are not saved when you close the browser. You could print the page: , solve the problems, then enter all your answers at the end.
📗 Please do not refresh the page: your answers will not be saved.
📗 Please report any bugs on Piazza: Link
# Warning: please enter your ID before you start!
# Question 11
📗 [3 points] The RDA Corporation has a prison with many cells. Without justification, you're about to be randomly thrown into a cell with equal probability. Cells to have Toruks that eat prisoners. Cells to are safe. With sufficient bribe, the warden will answer your question "Will I be in cell 1?" What's the mutual information (we call it information gain) between the warden's answer and your encounter with the Toruks? (I didn't write the stories in these questions, so I don't know the reference too.)
Hint
See Fall 2012 Final Q5, Fall 2011 Midterm Q5. Compute the information gain based on entropy of Toruks (call it \(Y\) where \(Y = 1\) is the event that there is a Toruk in the cell) and conditional entropy of Toruks given whether you are in cell 1 (call it \(Y | X\) where \(X = 1\) is the event that you are in cell 1). Then the information gain is \(I = H\left(Y\right) - H\left(Y | X\right)\), where \(H\left(Y\right) = -\mathbb{P}\left\{Y = 0\right\} \log_{2}\left(\mathbb{P}\left\{Y = 0\right\}\right) - \mathbb{P}\left\{Y = 1\right\} \log_{2}\left(\mathbb{P}\left\{Y = 1\right\}\right)\) and \(H\left(Y | X\right) = \mathbb{P}\left\{X = 0\right\} H\left(Y | X = 0\right) + \mathbb{P}\left\{X = 1\right\} H\left(Y | X = 1\right)\) where \(H\left(Y | X = 0\right) = -\mathbb{P}\left\{Y = 0 | X = 0\right\} \log_{2}\left(\mathbb{P}\left\{Y = 0 | X = 0\right\}\right) - \mathbb{P}\left\{Y = 1 | X = 0\right\} \log_{2}\left(\mathbb{P}\left\{Y = 1 | X = 0\right\}\right)\) and \(H\left(Y | X = 1\right) = -\mathbb{P}\left\{Y = 0 | X = 1\right\} \log_{2}\left(\mathbb{P}\left\{Y = 0 | X = 1\right\}\right) - \mathbb{P}\left\{Y = 1 | X = 1\right\} \log_{2}\left(\mathbb{P}\left\{Y = 1 | X = 1\right\}\right)\). Here, \(\mathbb{P}\left\{Y = 1\right\}\) is the probability that there is a Toruk (i.e. the number of Toruks divided by the number of cells), \(\mathbb{P}\left\{X = 1\right\}\) is the probability that you are in cell 1 (i.e. 1 divided by the number of cells), \(\mathbb{P}\left\{Y = 1 | X = 1\right\}\) is the probability that there is a Toruk given you are in cell 1 (which is always 1), and \(\mathbb{P}\left\{Y = 1 | X = 0\right\}\) is the probability that there is a Toruk given you are not in cell 1 (i.e. the number of Toruks not in cell 1 divided by the number of cells that are not cell 1).📗 Answer: .
📗 [3 points] Consider a training set with 8 items. The first dimension of their feature vectors are: . However, this dimension is continuous (i.e. it is a real number). To build a decision tree, one may ask questions in the form "Is \(x_{1} \geq \theta\)"? where \(\theta\) is a threshold value. Ideally, what is the maximum number of different \(\theta\) values we should consider for the first dimension \(x_{1}\)? Count the values of \(\theta\) such that all instances belong to one class.
Hint
See Fall 2016 Final Q11. At most one threshold between two consecutive distinct values is needed, for example, if the possible values are \([-1, 0, 1]\), at most one threshold less than \(-1\), one threshold between \(-1\) and \(0\), one threshold between \(0\) and \(1\), and one threshold larger than \(0\) are needed (four in total).📗 Answer: .
📗 [3 points] A decision tree has depth \(d\) = (a decision tree where the root is a leaf node has \(d\) = 0). All its internal node have \(b\) = children. The tree is also complete, meaning all leaf nodes are at depth \(d\). If we require each leaf node to contain at least training examples, what is the minimum size of the training set?
Hint
See Fall 2014 Midterm Q9, Fall 2012 Final Q6. The total number of leaf nodes in a complete tree is \(b^{d}\), and if at least \(n\) training examples are needed in each one of them, since the same training example cannot appear in multiple subtrees, there should be at least \(n b^{d}\) training examples in total.📗 Answer: .
📗 [3 points] Consider binary classification in 2D where the intended label of a point \(x = \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix}\) is positive (1) if \(x_{1} > x_{2}\) and negative (0) otherwise. Let the training set be all points of the form \(x\) = where \(a, b\) are integers. Each training item has the correct label that follows the rule above. With a 1NN (Nearest Neighbor) classifier (Euclidean distance), which ones of the following points are labeled positive? The drawing is not graded.
Hint
See Fall 2013 Final Q5, Fall 2011 Midterm Q3. If multiple instances have the same distance to the new point, use the instances with larger x values. This question should not be solved by finding the nearest training instance for each choice: you should draw the decision boundary and check which side the points are on.📗 Choices:
None of the above
📗 Calculator: .
📗 [3 points] Consider points in 2D and binary labels. Given the training data in the table, and use Manhattan distance with 1NN (Nearest Neighbor), which of the following points in 2D are classified as 1? Answer the question by first drawing the decision boundaries. The drawing is not graded.
| index | \(x_{1}\) | \(x_{2}\) | label |
| 1 | -1 | -1 | |
| 2 | -1 | 1 | |
| 3 | 1 | -1 | |
| 4 | 1 | 1 |
Hint
See Spring 2018 Question 7, Fall 2014 Midterm Q2, Fall 2012 Final Q4. As discussed in the lectures, if multiple instances have the same distance to the new point, use the ones with smaller indices. This question should not be solved by finding the nearest training instance for each choice: you should draw the decision boundary and check which side the points are on.📗 Choices:
None of the above
📗 [4 points] You are given a training set of five points and their 2-class classifications (+ or -): (, +), (, +), (, -), (, -), (, -). What is the decision boundary associated with this training set using 3NN (3 Nearest Neighbor)?
Hint
See Spring 2017 Midterm Q6. The decision boundary is the threshold such that all points on its left is classified as positive, and all points on its right is classified as negative. The threshold should be equidistant from the first and fourth points (i.e. the midpoint between the first and fourth points).📗 Answer: .
📗 [3 points] Let a dataset consist of \(n\) = points in \(\mathbb{R}\), specifically, the first \(n - 1\) points are and the last point \(x_{n}\) is unknown. What is the smallest value of \(x_{n}\) above which \(x_{n-1}\) is among \(x_{n}\)'s 3-nearest neighbors, but \(x_{n}\) is NOT among \(x_{n-1}\)'s 3-nearest neighbor? Note that the 3-nearest neighbors of a point in the training set include the point itself.
Hint
See Fall 2017 Final Q18. Find \(x_{n}\) satisfying \(x_{n} - x_{n-1} > x_{n-1} - x_{n-3}\) so that the 3-nearest neighbors of \(x_{n-1}\) are \(x_{n-1}, x_{n-2}, x_{n-3}\) which does not include \(x_{n}\).📗 Answer: .
📗 [4 points] What is the convolution between the image and the filter using zero padding? The flipped filter is .
Hint
Use the convolution formula between matrix X and a k by k filter W that \(A_{i,j} = \displaystyle\sum_{s=-k}^{k} \displaystyle\sum_{t=-k}^{k} W_{s,t} X_{i-s,j-t}\) for every element (i,j) of the matrix X. Intuitively, flip the filter and take the dot product between the filter and the submatrix centered at each (i,j) to compute the convolution at (i,j).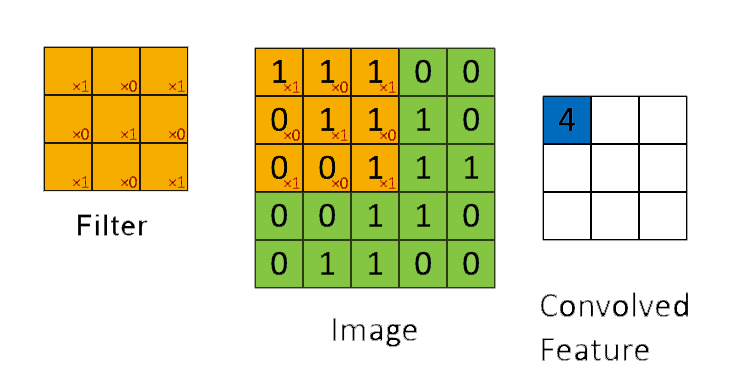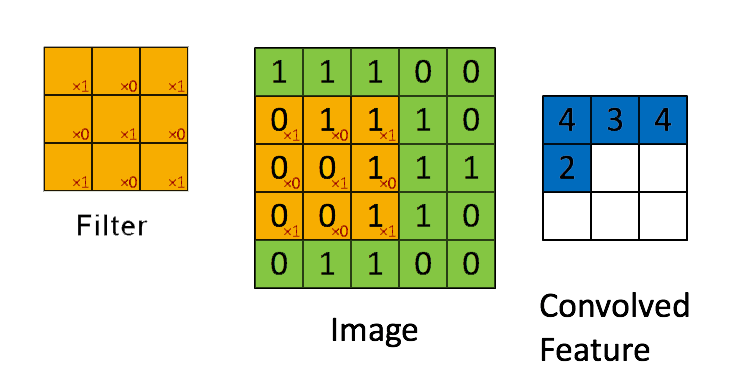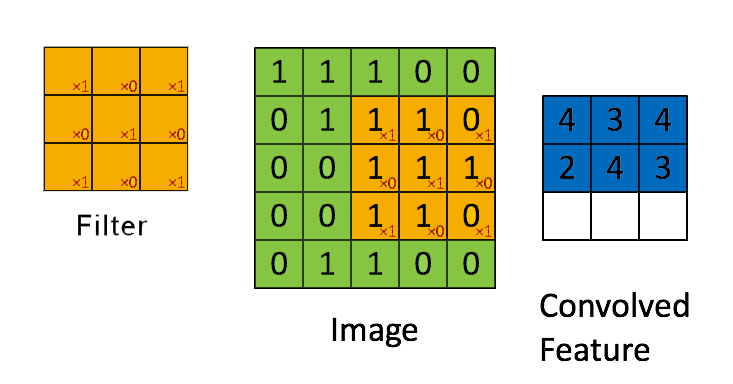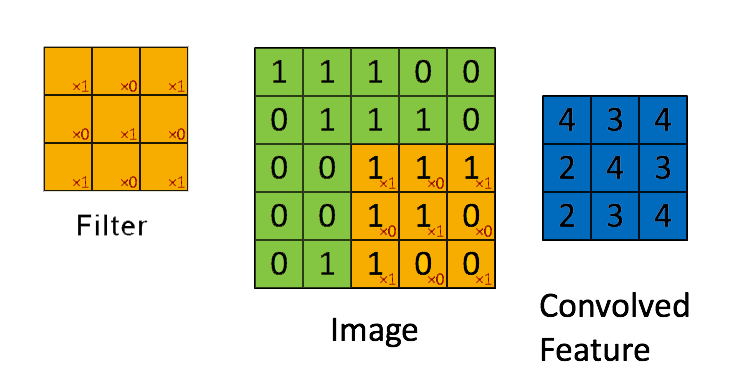
📗 Answer (matrix with multiple lines, each line is a comma separated vector): .
📗 [4 points] In a convolutional neural network, suppose the activation map of a convolution layer is . What is the activation map after a non-overlapping (stride 2) 2 by 2 max-pooling layer?
Hint
Take the maximum (or average) of each 2 by 2 submatrix and put them in a larger matrix.📗 Answer (matrix with multiple lines, each line is a comma separated vector): .
📗 [4 points] A convolutional neural network has input image of size x that is connected to a convolutional layer that uses a x filter, zero padding of the image, and a stride of 1. There are activation maps. (Here, zero-padding implies that these activation maps have the same size as the input images.) The convolutional layer is then connected to a pooling layer that uses x max pooling, a stride of (non-overlapping, no padding) of the convolutional layer. The pooling layer is then fully connected to an output layer that contains output units. There are no hidden layers between the pooling layer and the output layer. How many different weights must be learned in this whole network, not including any bias.
Hint
See Fall 2019 Final Q15, Spring 2018 Midterm Q8 Q9 Q10 Q11, Fall 2017 Final Q5, Spring 2017 Final Q5, Fall 2017 Midterm Q9, Fall 2017 Midterm Q11. Each k by k filter in the first layer has \(k \times k\) weights, the number of such filters depend on the number of activation maps in the next layer. The pooling layers do not have weights, but the number of units in the next layer depends on the pooling filter size (reduces the units by a factor of the filter size). The last layer is fully connected, so the number of weights is the product between the number of units in the previous layer and the number of output units.📗 Answer: .
📗 [1 points] Please enter any comments and suggestions including possible mistakes and bugs with the questions and the auto-grading, and materials relevant to solving the questions that you think are not covered well during the lectures. If you have no comments, please enter "None": do not leave it blank.
📗 Answer: .
# Submission
📗 Please do not modify the content in the above text field: use the "Grade" button to update.
📗 Please wait for the message "Successful submission." to appear after the "Submit" button. If there is an error message or no message appears after 10 seconds, please save the text in the above text box to a file using the button or copy and paste it into a file yourself and submit it to Canvas Assignment M5. You could submit multiple times (but please do not submit too often): only the latest submission will be counted.
📗 You could load your answers from the text (or txt file) in the text box below using the button . The first two lines should be "##m: 5" and "##id: your id", and the format of the remaining lines should be "##1: your answer to question 1" newline "##2: your answer to question 2", etc. Please make sure that your answers are loaded correctly before submitting them.
# Solutions
Last Updated: January 19, 2026 at 9:18 PM