Prev: W10, Next: W12 , Practice Questions: M31 , Links: Canvas, Piazza, Zoom, TopHat (744662)
Tools
📗 Calculator:
📗 Canvas:
pen
📗 You can expand all TopHat Quizzes and Discussions: , and print the notes: , or download all text areas as text file: .
# Reinforcement Learning
📗 An agent interacts with an environment and receives a reward (or incurs a cost) based on the state of the environment and the agent's action.
📗 The goal of reinforcement learning is to maximize the cumulative reward by learning the optimal actions in every state.
📗 Unlike search problems, the agent needs to learn the reward or cost function.
➩ Board games: Link.
➩ Video games: Link.
➩ Autonomous vehicle control: Link.
➩ Economic models: Link.
➩ Large language models (RLHF: Reinforcement Learning from Human Feedback): Link.
# Multi Armed Bandit
📗 A simple reinforcement learning problem where the state does not change is called the multi-armed bandit: Wikipedia.
➩ Multi-armed bandits.
➩ Clinical trials.
➩ Stock selection.
📗 There is a set of actions \(1, 2, ..., K\), reward from action \(k\) follows some distribution with mean \(\mu_{k}\), for example normal distribution with mean \(\mu_{k}\) and fixed variance \(\sigma^{2}\), or \(r \sim N\left(\mu_{k}, \sigma^{2}\right)\).
📗 The agent's goal is to maximize the total reward from repeatedly taking an action in \(T\) rounds.
➩ Reward maximization: \(\displaystyle\max_{a_{1}, a_{2}, ..., a_{T}} \left(r_{1}\left(a_{1}\right) + r_{2}\left(a_{2}\right) + ... + r_{T}\left(a_{T}\right)\right)\).
➩ Regret minimization: \(\displaystyle\min_{a_{1}, a_{2}, ..., a_{T}} \left(\displaystyle\max_{k} \mu_{k} - \dfrac{1}{T} \left(r_{1}\left(a_{1}\right) + r_{2}\left(a_{2}\right) + ... + r_{T}\left(a_{T}\right)\right)\right)\).
📗 An algorithm is called no-regret if as \(T \to \infty\), the regret approaches \(0\) with probability \(1\): Wikipedia.
TopHat Discussion
ID:📗 [1 points] The boxes have different mean rewards between 0 and 1. Click on one of them to collect the reward from the box. The goal is to maximize the total reward (or minimize the regret) given a fixed number of clicks. You have clicks left. Your current total reward is . Refresh the page to restart. Which box has the largest mean reward?
📗 Answer: .
# Exploration vs Exploitation
📗 There is a trade-off between taking actions for exploration vs exploitation:
➩ Exploration: taking actions to get more information (e.g. figure out the expected reward from each action).
➩ Exploitation: taking actions to get the highest rewards based on existing information (e.g. take the best action based on the current estimates of rewards).
📗 Epsilon-first strategy: \(\varepsilon T\) rounds of pure exploration, then use the empirically best in the remaining \(\left(1 - \varepsilon\right) T\) rounds.
➩ Empirically best action is \(\mathop{\mathrm{argmax}}_{k} \hat{\mu}_{k}\), where \(\hat{\mu}_{k}\) is the average reward from rounds where action \(k\) is used.
📗 Epsilon-greedy strategy: in every round, use the empirically best action with probability \(1 - \varepsilon\), and use a random action with probability \(\varepsilon\).
# Upper Confidence Bound
📗 The "best" action (based on current information) can also be defined based on the principle of optimism under uncertainty.
📗 An optimistic guess of the average reward (adjusted for uncertainty) in period \(t\) is \(\hat{\mu}_{k} + c \sqrt{\dfrac{2 \log\left(t\right)}{n_{k}}}\), where \(n_{k}\) is the number of rounds action \(k\) is used.
➩ This term \(\sqrt{\dfrac{2 \log\left(t\right)}{n_{k}}}\) represents the amount of uncertainty in the estimate \(\hat{\mu}_{k}\), the more action \(k\) is explored (higher \(n_{k}\)), the smaller the value of this term.
📗 The algorithm that always uses the action with the highest UCB is called the UCB1 algorithm: Wikipedia.
Math Note
📗 Technically, \(\sqrt{\dfrac{2 \log\left(t\right)}{n_{k}}}\) is half of the width of the confidence interval computed based on Hoeffding's inequality: Wikipedia.
TopHat Discussion
ID:📗 [1 points] The boxes have different mean rewards between 0 and 1. Click on one of them to collect the reward from the box. The goal is to maximize the total reward (or minimize the regret) given a fixed number of clicks. You have clicks left. Your current total reward is . Refresh the page to restart. Which box has the largest mean reward?
📗 Answer: .
# Markov Decision Process
📗 Reinforcement learning problem with multiple states is usually represented by Markov Decision Processes (MDP): Link, Wikipedia.
📗 Markov property on states and actions are assumed: \(\mathbb{P}\left\{s_{t+1} | s_{t}, a_{t}, s_{t-1}, a_{t-1}, ...\right\} = \mathbb{P}\left\{s_{t+1} | s_{t}, a_{t}\right\}\). The state in round \(t+1\), \(s_{t+1}\) only depends on the state and action in round \(t\), \(s_{t}\) and \(a_{t}\).
📗 The goal is learn a policy \(\pi\) to choose action \(\pi\left(s_{t}\right)\) that maximize the total expected discounted rewards: \(\mathbb{E}\left[r_{t} + \beta r_{t+1} + \beta^{2} r_{t+2} + ...\right]\).
➩ The reason a discount factor is used is so that the infinity sum is finite.
➩ Note that if the rewards are between \(0\) and \(1\), then the discounted total rewards is less than \(1 + \beta + \beta^{2} + ... = \dfrac{1}{1 - \beta}\).
Math Note
📗 To compute the sum, \(S = 1 + \beta + \beta^{2} + ...\), note that \(\beta S = \beta + \beta^{2} + \beta^{3} + ...\), so \(\left(1 - \beta\right) S = 1\) or \(S = \dfrac{1}{1 - \beta}\).
➩ This requires \(0 \leq \beta < 1\).
# Value Function
📗 The value function is the expected discounted reward given a policy function \(\pi\), or \(V^{\pi}\left(s_{t}\right) = \mathbb{E}\left[r_{t}\right] + \beta \mathbb{E}\left[r_{t+1}\right] + \beta^{2} \mathbb{E}\left[r_{t+2}\right] + ...\), where \(r_{t}\) is generated based on \(\pi\).
➩ To be precise, \(V^{\pi}\left(s_{t}\right) = \mathbb{E}\left[r_{t} | s_{t}, \pi\right] + \beta \mathbb{E}\left[r_{t+1} | s_{t}, \pi\right] + \beta^{2} \mathbb{E}\left[r_{t+2} | s_{t}, \pi\right] + ...\).
📗 The value function is the (only) function that satisfies the Bellman's equation: \(V^{\pi}\left(s_{t}\right) = \mathbb{E}\left[r_{t} | s_{t}, \pi\right] + \beta \mathbb{E}\left[V^{\pi}\left(s_{t+1}\right) | s_{t}, \pi\right]\).
📗 The optimal policy \(\pi^\star\) is the policy that maximizes the value function at every state.
# Q Function
📗 The Q function is the value function given a specific action in the current period (and follows \(\pi\) in future periods).
➩ By definition, \(Q^{\pi}\left(s_{t}, a_{t}\right) = \mathbb{E}\left[r_{t} | s_{t}, a_{t}\right] + \beta \mathbb{E}\left[r_{t+1} | s_{t}, a_{t}, \pi\right] + \beta^{2} \mathbb{E}\left[r_{t+2} | s_{t}, a_{t}, \pi\right] + ...\), which can be written as \(Q^{\pi}\left(s_{t}, a_{t}\right) = \mathbb{E}\left[r_{t} | s_{t}, a_{t}\right] + \beta \mathbb{E}\left[V^{\pi}\left(s_{t+1}\right) | s_{t}, a_{t}, \pi\right]\).
📗 Under the optimal policy, the Bellman's equation is satisfied: \(Q^\star\left(s_{t}, a_{t}\right) = \mathbb{E}\left[r_{t} | s_{t}, a_{t}\right] + \beta \mathbb{E}\left[V^\star\left(s_{t+1}\right) | s_{t}, a_{t}\right]\), for every state and action, where \(V^\star\left(s_{t+1}\right) = \displaystyle\max_{a} Q^\star\left(s_{t+1}, a\right)\).
📗 Bellman's equation can be used to iteratively solve for the Q function:
➩ Initialize \(\hat{Q}\left(s_{t}, a_{t}\right)\) for every state and action.
➩ Update \(\hat{Q}\left(s_{t}, a_{t}\right) \leftarrow \mathbb{E}\left[r_{t} | s_{t}, a_{t}\right] + \beta \mathbb{E}\left[\displaystyle\max_{a} \hat{Q}\left(s_{t+1}, a\right)\right]\).
➩ \(\hat{Q}\) converges to \(Q^\star\) given any initialization, assuming \(0 \leq \beta < 1\).
TopHat Discussion
ID:📗 [1 points] Compute the optimal policy (at each state the car can go Up, Down, Left, Right, or Stay). The color represents the reward from moving to each state (more red means more negative and more blue means more positive). Click on the plot on the right to update the Q function once. The discount factor is .
📗 Q Function (columns are U, D, L, R, S):
📗 V Function:
📗 Policy:
TopHat Quiz
(Past Exam Question) ID:📗 [4 points] Consider the following Markov Decision Process. It has two states \(s\), A and B. It has two actions \(a\): move and stay. The state transition is deterministic: "move" moves to the other state, while "stay" stays at the current state. The reward \(r\) is for move (from A and B), for stay (in A and B). Suppose the discount rate is \(\beta\) = .
Find the Q function in the format described by the following table. Enter a two by two matrix.
| State \ Action | stay | move |
| A | ? | ? |
| B | ? | ? |
📗 Answer (matrix with multiple lines, each line is a comma separated vector): .
# Q Learning
📗 The Q function can be learned by iteratively update the Q function using the Bellman's equation: Link, Wikipedia.
➩ \(\hat{Q}\left(s_{t}, a_{t}\right) = \left(1 - \alpha\right) \hat{Q}\left(s_{t}, a_{t}\right) + \alpha \left(r_{t} + \beta \displaystyle\max_{a} \hat{Q}\left(s_{t+1}, a\right)\right)\), where \(\alpha\) is the learning rate and is sometimes set to \(\dfrac{1}{1 + n\left(s_{t}, a_{t}\right)}\), \(n\left(s_{t}, a_{t}\right)\) is the number of visits to state \(s_{t}\) and action \(a_{t}\) in the past.
📗 Under certain assumptions, Q learning converges to the correct (optimal) Q function, and the optimal policy can be obtained by: \(\pi\left(s_{t}\right) = \mathop{\mathrm{argmax}}_{a} Q^\star\left(s_{t}, a\right)\) for every state.
TopHat Discussion
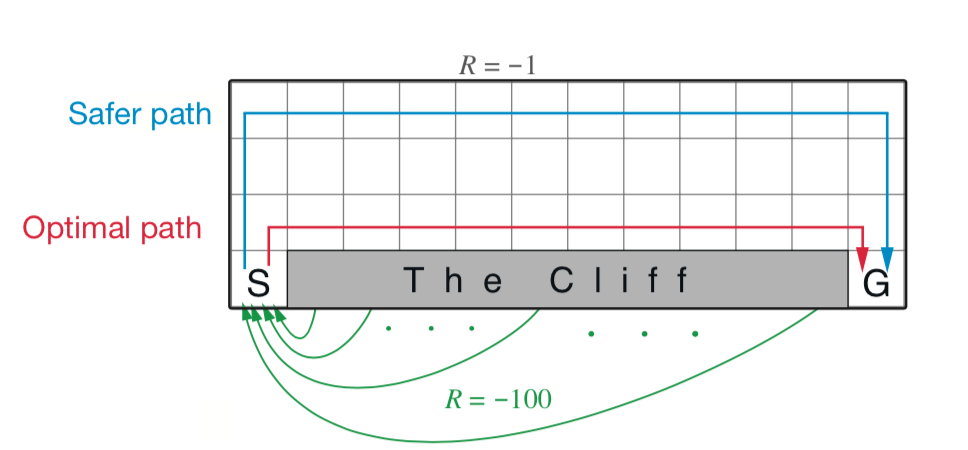
📗 [1 points] Compute the optimal policy (at each state the agent can go Up, Down, Left, Right). Falling into the cliff (black) leads to a loss of \(-100\) and walking (white) anywhere else leads to a loss of \(-1\). The agent starts at the blue tile and stops at the green tile.
📗 Click on the plot on the left to update the Q function times using Q learning. The plot on the right shows the number of visits to each square.
Epsilon greedy: \(\varepsilon\) = 0.1
Learning rate: \(\alpha\) = 0.1 or use \(\alpha = \dfrac{1}{1+n}\)
📗 Q Function (columns are U, D, L, R):
📗 V Function:
📗 Policy:
# SARSA
📗 An alternative to Q learning is SARSA (State Action Reward State Action). It uses a pre-specified action for the next period instead of the optimal action based on the current Q estimate: Wikipedia.
➩ \(\hat{Q}\left(s_{t}, a_{t}\right) = \left(1 - \alpha\right) \hat{Q}\left(s_{t}, a_{t}\right) + \alpha \left(r_{t} + \beta \hat{Q}\left(s_{t+1}, a_{t+1}\right)\right)\).
📗 The main difference is the action used in state \(s_{t+1}\).
➩ Q learning is an off-policy learning algorithm since \(a_{t+1}\) is the optimal policy in the next period, not a pre-specified policy (the Q function during learning does not correspond to any policy).
➩ SARSA is an on-policy learning algorithm since it computes the Q function based on a fixed policy.
TopHat Discussion
📗 [1 points] Compute the optimal policy (at each state the agent can go Up, Down, Left, Right). Falling into the cliff (black) leads to a loss of \(-100\) and walking (white) anywhere else leads to a loss of \(-1\). The agent starts at the blue tile and stops at the green tile.
📗 Click on the plot on the left to update the Q function times using Q learning. The plot on the right shows the number of visits to each square.
Epsilon greedy: \(\varepsilon\) = 0.1
Learning rate: \(\alpha\) = 0.1 or use \(\alpha = \dfrac{1}{1+n}\)
📗 Q Function (columns are U, D, L, R):
📗 V Function:
📗 Policy:

# Exploration vs Exploitation
📗 The policy used to generate the data for Q learning or SARSA can be Epsilon Greedy or UCB (requires some modification for MDPs).
➩ Epsilon greedy: with probability \(\varepsilon\), \(a_{t}\) is chosen uniformly randomly among all actions; with probability \(1-\varepsilon\), \(a_{t} = \mathop{\mathrm{argmax}}_{a} \hat{Q}\left(s_{t}, a\right)\).
📗 The choice of action can be randomized too: \(\mathbb{P}\left\{a_{t} | s_{t}\right\} = \dfrac{c^{\hat{Q}\left(s_{t}, a_{t}\right)}}{c^{\hat{Q}\left(s_{t}, 1\right)} + c^{\hat{Q}\left(s_{t}, 2\right)} + ... + c^{\hat{Q}\left(s_{t}, K\right)}}\), where \(c\) is a parameter controlling the trade-off between exploration and exploitation.
test mab,ucb,car,ql,qcl,scl q
📗 Notes and code adapted from the course taught by Professors Jerry Zhu, Yingyu Liang, and Charles Dyer.
📗 Please use Ctrl+F5 or Shift+F5 or Shift+Command+R or Incognito mode or Private Browsing to refresh the cached JavaScript.
📗 If you missed the TopHat quiz questions, please submit the form: Form.
📗 Anonymous feedback can be submitted to: Form.
Prev: W10, Next: W12
Last Updated: November 21, 2025 at 11:41 PM